题目内容
(12分)已知圆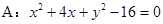 及定点
及定点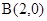 ,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足
,点Q是圆A上的动点,点G在BQ上,点P在QA上,且满足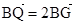 ,
,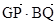 =0.
=0.
(I)求P点所在的曲线C的方程;
(II)过点B的直线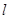 与曲线C交于M、N两点,直线
与曲线C交于M、N两点,直线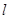 与y轴交于E点,若
与y轴交于E点,若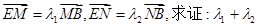 为定值。
为定值。
(I)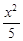 +y2=1;(ⅡI)见解析.
+y2=1;(ⅡI)见解析.
【解析】(1)由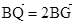 ,
,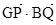 =0得
=0得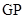 垂直平分线段
垂直平分线段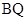 ,
,
即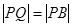 ,所以
,所以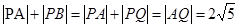 ,根据椭圆的定义得曲线C的方程;
,根据椭圆的定义得曲线C的方程;
(2)利用点M、N在椭圆上, 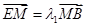 ,
,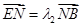 可得到
可得到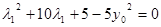 ,
,
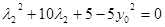 .
.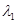 ,
,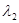 是方程
是方程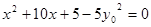 的两个根,∴
的两个根,∴  .
.
也可以设出直线 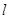 的方程,与椭圆
的方程,与椭圆 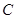 的方程联立,求出
的方程联立,求出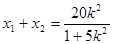 ,
, .由
.由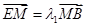 ,
,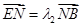 可得到
可得到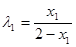 ,
,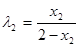 整理
整理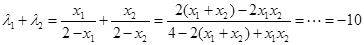
∵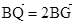 ,
,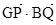 =0∴
=0∴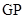 垂直平分线段
垂直平分线段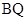 ,
,
即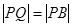 ,所以
,所以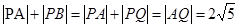 ,由椭圆定义:
,由椭圆定义:
曲线C的方程为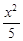 +y2=1 5分
+y2=1 5分
(Ⅱ)证法1:设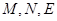 点的坐标分别为
点的坐标分别为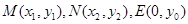 ,
,
又易知 点的坐标为
点的坐标为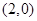 .且点B在椭圆C内,故过点B的直线l必与椭圆C相交.
.且点B在椭圆C内,故过点B的直线l必与椭圆C相交.
∵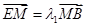 ,∴
,∴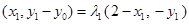 .
.
∴
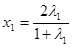 ,
, . 7分
. 7分
将M点坐标代入到椭圆方程中得: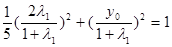 ,
,
去分母整理,得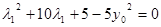 . 10分
. 10分
同理,由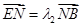 可得:
可得: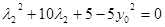 .
.
∴
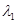 ,
,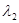 是方程
是方程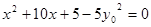 的两个根,
的两个根,
∴
 . 12分
. 12分
(Ⅱ)证法2:设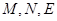 点的坐标分别为
点的坐标分别为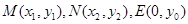 ,又易知
,又易知 点的坐标为
点的坐标为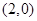 .且点B在椭圆C内,故过点B的直线l必与椭圆C相交.
.且点B在椭圆C内,故过点B的直线l必与椭圆C相交.
显然直线 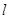 的斜率存在,设直线
的斜率存在,设直线 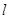 的斜率为
的斜率为 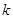 ,则直线
,则直线
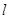 的方程是
的方程是 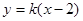 .
.
将直线 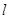 的方程代入到椭圆
的方程代入到椭圆 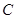 的方程中,消去
的方程中,消去 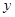 并整理得
并整理得
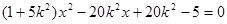 . 8分
. 8分
∴
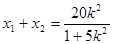 ,
, .
.
又 ∵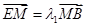 ,
,
则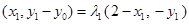 .∴
.∴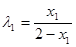 ,
,
同理,由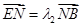 ,∴
,∴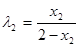 . 10分
. 10分
∴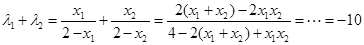 . 12分
. 12分

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
 及定点
及定点 ,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足
,点P是圆M上的动点,点Q在NP上,点G在MP上,且满足
 与曲线C交于A、B两点,O是坐标原点,设
与曲线C交于A、B两点,O是坐标原点,设 是否存在这样的直线
是否存在这样的直线