题目内容
四棱锥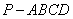 底面是菱形,
底面是菱形,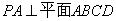 ,
,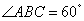 ,
,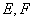 分别是
分别是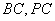 的中点.
的中点.
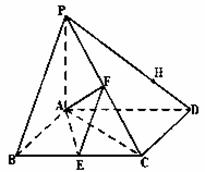
(1)求证:平面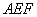 ⊥平面
⊥平面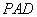 ;
;
(2)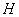 是
是 上的动点,
上的动点,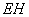 与平面
与平面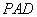 所成的最大角为
所成的最大角为 ,求二面角
,求二面角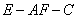 的正切值.
的正切值.


(2)过E作EQ⊥AC,垂足为Q,过作QG⊥AF,垂足为G,连GE,∵PA⊥面ABCD,∴PA⊥EQ,EQ⊥面PAC,则∠EGQ是二面角E-AF-C的平面角.
过点A作AH⊥PD,连接EH,∵AE⊥面PAD,∴∠AHE是EH与面PAD所成的最大角.
∵∠AHE= ,∴AH=AE=
,∴AH=AE= ,AH﹒PD=PA﹒AD,2a﹒PA=
,AH﹒PD=PA﹒AD,2a﹒PA= ﹒
﹒ ,PA=2
,PA=2 ,PC=4a,EQ=
,PC=4a,EQ= ,CQ=
,CQ= ,GQ=
,GQ= ,tan∠EGQ=
,tan∠EGQ= .
.
【考点定位】1.面面垂直的判定.2.动点问题.3.二面角问题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
已知向量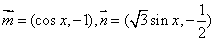 ,设函数
,设函数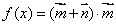 .
.
(1).求函数f(x)的最小正周期;
(2).已知a,b,c分别为三角形ABC的内角对应的三边长,A为锐角,a=1, ,且
,且 恰是函数f(x)在
恰是函数f(x)在 上的最大值,求A,b和三角形ABC的面积.
上的最大值,求A,b和三角形ABC的面积.
 满足:
满足: ,若存在两项
,若存在两项 使得
使得 ,则
,则 的最小值为( )
的最小值为( ) 
 B.
B. C.
C. D.不存在
D.不存在 中,
中, ,
, 为
为 的中点.将
的中点.将 沿
沿 折起,使得平面
折起,使得平面 平面
平面 .
. ;
; 是线段
是线段 上的一动点,问点E在何位置时,二面角
上的一动点,问点E在何位置时,二面角 的余弦值为
的余弦值为 .
.
 ,以右顶点为圆心,实半轴长为半径的圆被双曲线的一条渐近线分为弧
,以右顶点为圆心,实半轴长为半径的圆被双曲线的一条渐近线分为弧 长为1:2的两部分,则双曲线的离心率为( )
长为1:2的两部分,则双曲线的离心率为( ) B.
B.  C.
C.  D.
D. 
 在一个周期内的图象如右,此函数的解析式为( )
在一个周期内的图象如右,此函数的解析式为( )
 B.
B.
 D.
D.
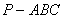 中,直线
中,直线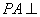 平面
平面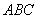 ,且
,且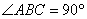 ,又点
,又点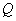 ,
,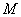 ,
,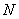 分别是线段
分别是线段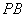 ,
,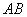 ,
,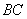 的中点,且点
的中点,且点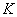 是线段
是线段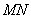 上的动点.
上的动点.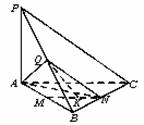
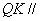 平面
平面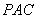 ;
;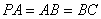 ,求二面角
,求二面角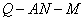 的平面角的余弦值.
的平面角的余弦值. 的图象向左平移
的图象向左平移 个单位长度后得到函数
个单位长度后得到函数 ,则函数
,则函数