题目内容
已知椭圆 ,
, 、
、 是其左右焦点,离心率为
是其左右焦点,离心率为 ,且经过点
,且经过点 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)若 、
、 分别是椭圆长轴的左右端点,
分别是椭圆长轴的左右端点, 为椭圆上动点,设直线
为椭圆上动点,设直线
 斜率为
斜率为 ,且
,且 ,求直线
,求直线 斜率的取值范围;
斜率的取值范围;
(3)若 为椭圆上动点,求
为椭圆上动点,求 的最小值.
的最小值.
【答案】
(1)椭圆 的方程为
的方程为 ;(2)直线
;(2)直线 的斜率的取值范围是
的斜率的取值范围是 ;
;
(3) 的最小值是
的最小值是 .
.
【解析】
试题分析:(1)利用离心率以及 确定
确定 、
、 之间的等量关系,然后将点
之间的等量关系,然后将点 的坐标代入椭圆
的坐标代入椭圆 的方程求出
的方程求出 、
、 ,从而确定椭圆
,从而确定椭圆 的标准方程;(2)设直线
的标准方程;(2)设直线 的斜率为
的斜率为 ,并设点
,并设点 的坐标为
的坐标为 ,利用点
,利用点 在椭圆上以及斜率公式得到
在椭圆上以及斜率公式得到 ,进而利用
,进而利用 的取值范围可以求出
的取值范围可以求出 的取值范围;(3)利用已知条件
的取值范围;(3)利用已知条件 ,利用余弦定理得到
,利用余弦定理得到 ,结合基本不等式求出
,结合基本不等式求出 的最小值.
的最小值.
试题解析:(1) ,故椭圆
,故椭圆 的方程为
的方程为 ;
;
(2)设 的斜率为
的斜率为 ,设点
,设点 ,
,
则 ,
, ,
,
 及
及 ,
,
则 =
= 又
又 ,
,
 ,故
,故 斜率的取值范围为
斜率的取值范围为 ;
;
(3)设椭圆的半长轴长、半短轴长、半焦距分别为 、
、 、
、 ,则有
,则有
 ,
, ,
, ,
, ,
,
由椭圆定义,有 ,
,




 的最小值为
的最小值为 .
.
(当且仅当 时,即
时,即 取椭圆上下顶点时,
取椭圆上下顶点时, 取得最小值)
取得最小值)
考点:1.椭圆的标准方程;2.点差法;3.余弦定理;4.基本不等式

练习册系列答案
相关题目
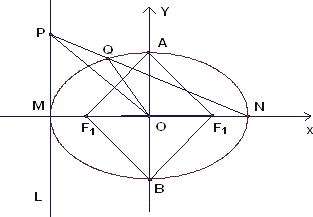 已知椭圆
已知椭圆 已知椭圆
已知椭圆