题目内容
（1）已知正数a、b满足a+b=1．求：
的最小值．（2）若正实数x、y满足x+y+3=xy，求xy的最小值．
【答案】分析：利用基本不等式的性质即可得出．
解答：解：（1）∵正数a+b=1，∴
=
=3+
=3+2
即为最小值，当且仅当a+b=1，
，即
，
时取等号；
（2）∵正实数x、y满足x+y+3=xy，∴
，化为
，∴
，即xy≥9，当且仅当x=y=3时取等号，∴xy的最小值为9．
点评：熟练掌握基本不等式的性质是解题的关键．注意“一正，二定，三相等”．
解答：解：（1）∵正数a+b=1，∴
==3+=3+2即为最小值，当且仅当a+b=1，，即，时取等号；（2）∵正实数x、y满足x+y+3=xy，∴
，化为，∴，即xy≥9，当且仅当x=y=3时取等号，∴xy的最小值为9．点评：熟练掌握基本不等式的性质是解题的关键．注意“一正，二定，三相等”．
练习册系列答案
相关题目
+
+
≥ 
＋b
+
+
≥1
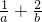的最小值．