题目内容
不等式选讲:已知x,y,z∈R,且x-2y-3z=4,求x2+y2+z2的最小值.
由柯西不等式,得[x+(-2)y+(-3)z]2≤[12+(-2)2+(-3)2](x2+y2+z2),
即(x-2y-3z)2≤14(x2+y2+z2),…(5分)
即16≤14(x2+y2+z2).
所以x2+y2+z2≥
,即x2+y2+z2的最小值为
.…(10分)
即(x-2y-3z)2≤14(x2+y2+z2),…(5分)
即16≤14(x2+y2+z2).
所以x2+y2+z2≥
| 8 |
| 7 |
| 8 |
| 7 |

练习册系列答案
相关题目
 [选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
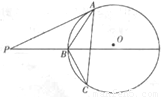
[选做题]在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内. 从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)
从A,B,C,D四个中选做2个A.选修4-1(几何证明选讲)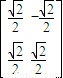 对应的变换作用下得到的曲线C′的方程.
对应的变换作用下得到的曲线C′的方程.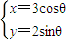 (θ为参数)和曲线C2:ρsin(θ-
(θ为参数)和曲线C2:ρsin(θ-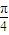 )=
)=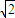 .
.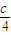 ,|y-b|<
,|y-b|<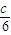 ,求证:|2x-3y-2a+3b|<c.
,求证:|2x-3y-2a+3b|<c.