Question

[选做题]在A、B、C、D四小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内．
A．（选修4-1：几何证明选讲）
过圆O外一点P分别作圆的切线和割线交圆于A，B，且PB=7，∠ABP=∠ABC，C是圆上一点使得BC=5，求线段AB的长．
B．（选修4-2：矩阵与变换）
求曲线C：xy=1在矩阵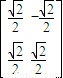对应的变换作用下得到的曲线C′的方程．
C．（选修4-4：坐标系与参数方程）
已知曲线C₁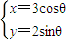：（θ为参数）和曲线C₂：ρsin（θ-）=．
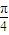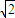（1）将两曲线方程分别化成普通方程；
（2）求两曲线的交点坐标．
D．（选修4-5：不等式选讲）
已知|x-a|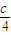＜，|y-b|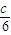＜，求证：|2x-3y-2a+3b|＜c．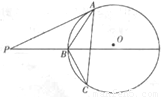

Answer 1

【答案】分析：A：根据同弧所对的圆周角与弦切角相等，得到∠C=∠BAP，根据所给的两个角相等，得到两个三角形相似，根据相似三角形对应边成比例，得到比例式，代入已知的长度，求出结果．
B：设P（x，y）为曲线xy=1上的任意一点，在矩阵A变换下得到另一点P'（x'，y'），根据法则 = ，求出即 x=（+），
y=（ - ）．再由x•y=1 可得  -=2，从而得到曲线C′的方程．
C：把参数方程化为普通方程，把极坐标方程化为直角坐标方程，联立方程组求得求两曲线的交点坐标．
D：由题意可得|2x-2a|＜，|3y-3b|＜，故|2x-2a|+|3y-3b|＜c．再根据绝对值不等式的性质可得|2x-3y-2a+3b|≤|2x-2a|+|3y-3b|，从而证得不等式．
解答：解：A：∵∠BAC=∠APB，∠C=∠BAP，∴△PAB∽△ACB，∴  AB²=PB•BC=7×5=35，∴AB=．
B：设P（x，y）为曲线xy=1上的任意一点，在矩阵A变换下得到另一点P'（x'，y'），
则有 = ，∴x′=（x-y），y′=（x+y），
即 x=（x′+y′），y=（ y′-x′ ）．
再由x•y=1可得 -=2，故的曲线C′的方程为y²-x²=1．
C：（1）把曲线C₁：（θ为参数），利用同角三角函数基本关系化为普通方程为 +=1． 
把曲线C₂：ρsin（θ-）= 即 ρsinθ-cosθ=，化为直角坐标为 x-y+2=0．
（2）由  解得 ，或 ，故两曲线的交点坐标为（0，2）或（-，）．
D：∵已知|x-a|＜，|y-b|＜，∴|2x-2a|＜，|3y-3b|＜，∴|2x-2a|+|3y-3b|＜c．
再由|2x-3y-2a+3b|=|（2x-2a）-（3y-3b）|≤|2x-2a|+|3y-3b|，
可得|2x-3y-2a+3b|＜c．
点评：本题可选圆的切线的性质的应用，考查同弧所对的圆周角等于弦切角，考查三角形相似的判断和性质．求曲线关于矩阵变换后的曲线方程．把参数方程化为普通方程的方法，把极坐标方程化为直角坐标方程的方法，求两曲线的交点坐标．绝对值不等式的性质应用，属于中档题．