题目内容
7.已知a>0,a≠1且a3>a2,已知函数f(x)=ax在区间[1,2]上的最大值与最小值之差为2,设函数$g(x)=1-\frac{2}{{{a^x}+1}}$.(1)判断函数g(x)的奇偶性;
(2)证明:$g({{x^2}-x+\frac{3}{4}})≥3-2\sqrt{2}$.
分析 (1)由指数函数的单调性,判断a>1,由最值可得a的方程,解得a=2,进而运用奇偶性的定义,计算g(-x),与g(x)比较,即可判断g(x)的奇偶性;
(2)判断g(x)在R上递增,配方法求出x2-x+$\frac{3}{4}$≥$\frac{1}{2}$,计算即可得证.
解答 解:∵a>0,a≠1,a3>a2,∴a>1,
又y=ax在[1,2]上为增函数,
∴a2-a=2,解得a=2或a=-1(舍去).
∴$g(x)=1-\frac{2}{{{2^x}+1}}=\frac{{{2^x}-1}}{{{2^x}+1}}$.
(1)函数g(x)的定义域为R,
且$g({-x})=\frac{{{2^{-x}}-1}}{{{2^{-x}}+1}}=\frac{{1-{2^x}}}{{{2^x}+1}}=-\frac{{{2^x}-1}}{{{2^x}+1}}=-g(x)$,
∴函数g(x)是奇函数.
(2)证明:由复合函数的单调性得函数g(x)在R上单调递增,
∵${x^2}-x+\frac{3}{4}={({x-\frac{1}{2}})^2}+\frac{1}{2}≥\frac{1}{2}$,
∴$g({{x^2}-x+\frac{3}{4}})≥g({\frac{1}{2}})=3-2\sqrt{2}$.
点评 本题考查函数的奇偶性和单调性的判断及运用:证明不等式,考查指数函数的单调性及应用,运用定义是解本题的关键,考查运算能力,属于中档题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
16.已知函数f(x)=asinx-bcosx(其中a,b为正实数)的图象关于直线$x=-\frac{π}{6}$对称,且?x1,x2∈R,x1≠x2,f(x1)f(x2)≤4恒成立,则下列结论正确的是( )
| A. | $a=\sqrt{3}$,b=1 | |
| B. | 函数f(x)在区间$[{\frac{π}{6},π}]$上单调递增 | |
| C. | 函数f(x)的图象的一个对称中心为$({\frac{2}{3}π,0})$ | |
| D. | 不等式f(x1)f(x2)≤4取到等号时|x2-x1|的最小值为2π |
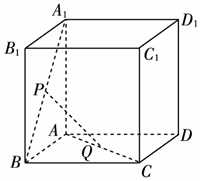 如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD对角线上的点,且A1P=AQ,证明:PQ∥平面BCC1B1.
如图所示,已知P、Q是单位正方体ABCD-A1B1C1D1的面A1B1BA和面ABCD对角线上的点,且A1P=AQ,证明:PQ∥平面BCC1B1.