题目内容
已知函数g(x)=aex-1-x2+bln(x+1),a,b∈R,
(Ⅰ)若a=0,b=1,求函数g(x)的单调区间;
(Ⅱ)若g(x)的图象在(0,g(0))处与直线x-ey+1=0相切,
(ⅰ)求a、b的值;
(ⅱ)求证:x∈(-1,1),g(x)<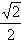 。
。
(Ⅰ)若a=0,b=1,求函数g(x)的单调区间;
(Ⅱ)若g(x)的图象在(0,g(0))处与直线x-ey+1=0相切,
(ⅰ)求a、b的值;
(ⅱ)求证:x∈(-1,1),g(x)<
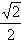 。
。 解:(Ⅰ)依题意,有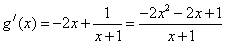 ,
,
令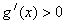 ,解得
,解得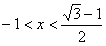 ;令
;令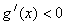 ,解得
,解得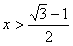 ,
,
所以增区间是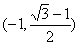 ,减区间是
,减区间是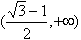 ;
;
(Ⅱ)(ⅰ)由切线方程可知:切点(0,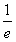 ),切线斜率为
),切线斜率为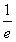 ,
,
所以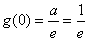 ,
,
因为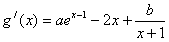 ,
,
所以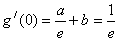 ,
,
综上,a=1,b=0;
(ⅱ)证明: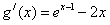 ,记
,记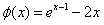 ,
,
在(-1,1)上,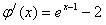 <0,
<0,
所以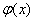 是减函数,即函数
是减函数,即函数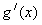 在(-1,1)上是减函数,
在(-1,1)上是减函数,
因为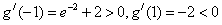 ,
,
所以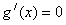 在(-1,1)内恰有一根,记为x0,
在(-1,1)内恰有一根,记为x0,
在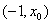 上,
上,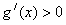 ,g(x)是增函数;在
,g(x)是增函数;在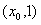 上,
上,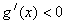 ,g(x)是减函数,
,g(x)是减函数,
所以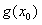 是极大值,也是最大值,
是极大值,也是最大值,
只需证明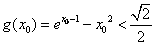 ,
,
因为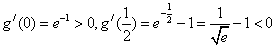 ,
,
所以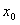
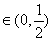 ,
,
所以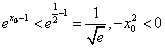 ,
,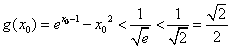 。
。
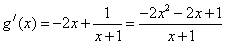 ,
,令
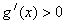 ,解得
,解得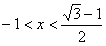 ;令
;令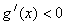 ,解得
,解得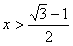 ,
,所以增区间是
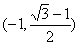 ,减区间是
,减区间是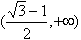 ;
;(Ⅱ)(ⅰ)由切线方程可知:切点(0,
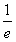 ),切线斜率为
),切线斜率为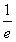 ,
,所以
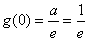 ,
,因为
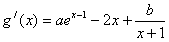 ,
,所以
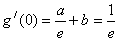 ,
,综上,a=1,b=0;
(ⅱ)证明:
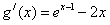 ,记
,记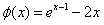 ,
,在(-1,1)上,
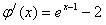 <0,
<0,所以
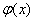 是减函数,即函数
是减函数,即函数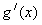 在(-1,1)上是减函数,
在(-1,1)上是减函数,因为
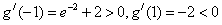 ,
,所以
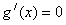 在(-1,1)内恰有一根,记为x0,
在(-1,1)内恰有一根,记为x0,在
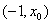 上,
上,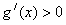 ,g(x)是增函数;在
,g(x)是增函数;在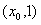 上,
上,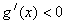 ,g(x)是减函数,
,g(x)是减函数,所以
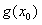 是极大值,也是最大值,
是极大值,也是最大值,只需证明
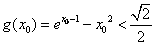 ,
,因为
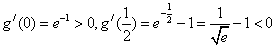 ,
,所以
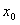
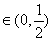 ,
,所以
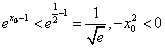 ,
,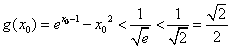 。
。
练习册系列答案
相关题目
