题目内容
已知函数![]() (
(![]() ,
,![]() 为正实数).
为正实数).
(Ⅰ)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)求函数![]() 的单调区间;
的单调区间;
(Ⅲ)若函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的取值范围.
的取值范围.
证明:(Ⅰ)因为平面![]() 平面
平面![]() ,
,
![]() ,且面
,且面![]() 面
面![]() ,
,
所以![]() 平面
平面![]() .
.
又因为![]() 平面
平面![]()
所以![]() . …………………………………………… 6分
. …………………………………………… 6分

(Ⅱ)由(Ⅰ)可知,![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() 平面
平面![]() .
.
即![]() ,
,![]() ,
,
所以![]() 为二面角
为二面角![]() 的平面角.
的平面角.
在![]() 中,
中, ![]() ,
,
所以二面角![]() 的大小
的大小![]() . …………………………………… 13分
. …………………………………… 13分
法二:取![]() 的中点
的中点![]() ,
, ![]() 的中点
的中点![]() .
.
在![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,所以,
的中点,所以,![]() .
.
又因为平面![]() 平面
平面![]() ,且平面
,且平面![]() 平面
平面![]()
所以,![]() 平面
平面![]() .显然,有
.显然,有![]() . ……………………………… 1分
. ……………………………… 1分
如图,以P为坐标原点,PA为x轴,PE为y轴,PS
为z轴建立空间直角坐标系,
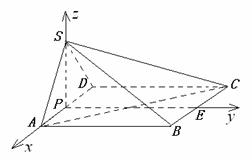
则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() . ………………………………………………………………3分
. ………………………………………………………………3分
(Ⅰ)易知![]()
因为![]() ,
,
所以![]() . …………………………………………………………… 6分
. …………………………………………………………… 6分
(Ⅱ)设![]() 为平面
为平面![]() 的一个法向量,则有
的一个法向量,则有![]() ,
,
即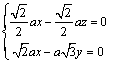 ,所以
,所以![]() . ……………………………… 7分
. ……………………………… 7分
显然,![]() 平面
平面![]() ,所以
,所以![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
所以![]() 为平面
为平面![]() 的一个法向量.……………………………………… 9分
的一个法向量.……………………………………… 9分
所以 ![]() ,
,
所以二面角![]() 的大小为
的大小为![]() . ………………………………………… 13分
. ………………………………………… 13分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,其中
,其中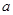 为正实数,
为正实数,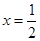 是
是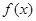 的一个极值点.
的一个极值点.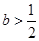 时,求函数
时,求函数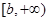 上的最小值.
上的最小值.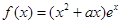 ,其中
,其中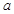 为正实数,
为正实数,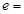 2.7182……
2.7182……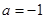 时,求
时,求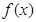 在点
在点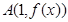 处的切线方程。
处的切线方程。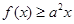 恒成立。
恒成立。 (
( ,
, 为正实数).
为正实数). ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; ,求
,求 (
( ,
, 为正实数).
为正实数). ,求曲线
,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间;
的单调区间; ,求
,求