题目内容
已知函数 ,其中
,其中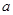 为正实数,
为正实数,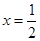 是
是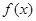 的一个极值点.
的一个极值点.
(Ⅰ)求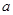 的值;
的值;
(Ⅱ)当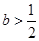 时,求函数
时,求函数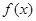 在
在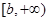 上的最小值.
上的最小值.
【答案】
(Ⅰ)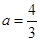 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)由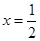 为函数
为函数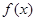 的一个极值点,得到
的一个极值点,得到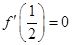 便可求出
便可求出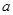 的值,但在求得答案后注意
的值,但在求得答案后注意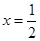 处附近左、右两侧导数符号相反,即成为极值点的必要性;(Ⅱ)对于含参函数的最值问题,一般结合导数考察函数在相应区间的单调性,利用端点值以及函数的极值确定函数的最小值.
处附近左、右两侧导数符号相反,即成为极值点的必要性;(Ⅱ)对于含参函数的最值问题,一般结合导数考察函数在相应区间的单调性,利用端点值以及函数的极值确定函数的最小值.
试题解析: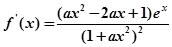
(Ⅰ)因为 是函数
是函数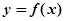 的一个极值点,
的一个极值点,
所以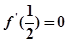 ,因此,
,因此,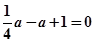 ,解得
,解得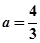 ,
,
经检验,当 时,
时,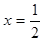 是
是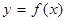 的一个极值点,故所求
的一个极值点,故所求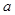 的值为
的值为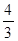 .
.
4分
(Ⅱ)由(Ⅰ)可知,
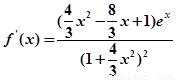
令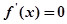 ,得
,得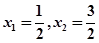
 与
与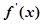 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以, 的单调递增区间是
的单调递增区间是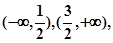 单调递减区间是
单调递减区间是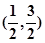
当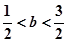 时,
时, 在
在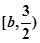 上单调递减,在
上单调递减,在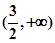 上单调递增
上单调递增
所以 在
在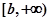 上的最小值为
上的最小值为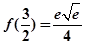
当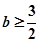 时,
时, 在
在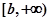 上单调递增,
上单调递增,
所以 在
在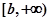 上的最小值为
上的最小值为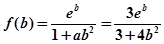
13分
考点:函数的极值、函数的单调性与最值

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目










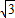 sinxcosx+cos2x+m,其中m为实常数.求f(x)的最小正周期、单调递增区间、所有的对称轴方程、值域.
sinxcosx+cos2x+m,其中m为实常数.求f(x)的最小正周期、单调递增区间、所有的对称轴方程、值域.