题目内容
在△ABC中,a,b,c分别是三内角A,B,C所对的三边,已知b2+c2=a2+bc.
(1)求角A的大小;
(2)若2sin2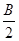 +2sin2
+2sin2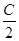 =1,试判断△ABC的形状.
=1,试判断△ABC的形状.
(1)求角A的大小;
(2)若2sin2
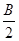 +2sin2
+2sin2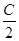 =1,试判断△ABC的形状.
=1,试判断△ABC的形状.(1) (2)等边三角形
(2)等边三角形
 (2)等边三角形
(2)等边三角形解:(1)∵b2+c2=a2+bc,
∴cosA= =
=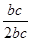 =
= ,得A=
,得A= .
.
(2)∵2sin2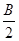 +2sin2
+2sin2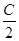 =1,
=1,
则1-cosB+1-cosC=1.
∴cosB+cosC=1,
即cosB+cos( -B)=1,得到sin(B+
-B)=1,得到sin(B+ )=1.
)=1.
∵0<B< ,∴
,∴ <B+
<B+ <
< .
.
∴B+ =
=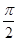 ,∴B=
,∴B= .
.
∴△ABC为等边三角形.
∴cosA=
 =
=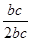 =
= ,得A=
,得A= .
.(2)∵2sin2
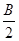 +2sin2
+2sin2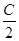 =1,
=1,则1-cosB+1-cosC=1.
∴cosB+cosC=1,
即cosB+cos(
 -B)=1,得到sin(B+
-B)=1,得到sin(B+ )=1.
)=1.∵0<B<
 ,∴
,∴ <B+
<B+ <
< .
.∴B+
 =
=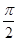 ,∴B=
,∴B= .
.∴△ABC为等边三角形.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
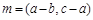 ,
,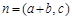 ,且
,且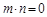
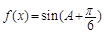 的值域.
的值域.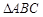 中,
中,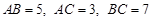 ,则
,则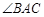 的大小为 .
的大小为 .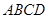 的内角
的内角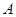 与
与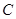 互补,
互补,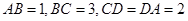 .
.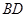 ;
;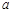 、
、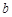 、
、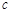 分别为
分别为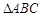 的三边,且
的三边,且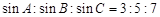 ,那么这个三角形的最大角等于
,那么这个三角形的最大角等于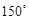

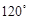

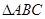 中,
中,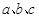 分别为角
分别为角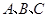 的对边,且满足
的对边,且满足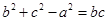 .
.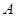 的值;
的值;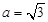 ,求bc最大值.
,求bc最大值. 中,已知
中,已知  ,则
,则 的大小为 .
的大小为 . ,则该三角形面积的最大值是( )
,则该三角形面积的最大值是( )