题目内容
在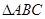 中,
中,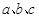 分别为角
分别为角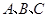 的对边,且满足
的对边,且满足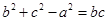 .
.
(1)求角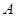 的值;
的值;
(2)若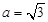 ,求bc最大值.
,求bc最大值.
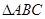 中,
中,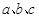 分别为角
分别为角 的对边,且满足
的对边,且满足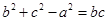 .
.(1)求角
 的值;
的值;(2)若
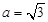 ,求bc最大值.
,求bc最大值.(1) ;(2)3
;(2)3
 ;(2)3
;(2)3试题分析:本题主要考查正弦定理、余弦定理的应用.在三角形中考虑问题时这两个定理用的最多.(1)先根据余弦定理求出角A的余弦值,然后可得到角A的值.(2)运用均值不等式得到
 代入到
代入到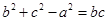 ,解得
,解得 的最大值.
的最大值.(1)∵
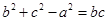 ,∴
,∴ 又
又 ,∴
,∴ ;
;(2)∵
 ,∴
,∴ ,又因为
,又因为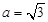 ∴
∴

练习册系列答案
相关题目
 .
.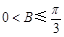 ;
;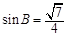 ,且
,且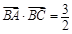 ,求
,求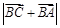 的值.
的值. 中,角
中,角 ,
, ,
, 的对边分别为
的对边分别为 ,
, ,
, ,若
,若 .
. ;
; ,
, 时,求
时,求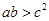 ,则
,则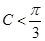 ;
;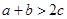 ,则
,则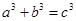 ,则
,则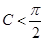 ;
;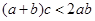 ,则
,则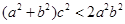 ,则
,则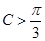 .
. 中,
中, 是三个内角
是三个内角 的对边,关于
的对边,关于 的不等式
的不等式
 的解集是空集.
的解集是空集. 的最大值;
的最大值; ,
, ,求当角
,求当角 的值.[
的值.[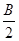 +2sin2
+2sin2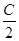 =1,试判断△ABC的形状.
=1,试判断△ABC的形状. 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,
, ,
, .
. 的值;(2) 设函数
的值;(2) 设函数 ,求
,求 的值.
的值. 船在灯塔
船在灯塔 北偏东
北偏东 处,且
处,且 ,
, 船在灯塔
船在灯塔 处,
处, 两船间的距离为
两船间的距离为
 =3,c=3
=3,c=3 ,A=30°,则角C等于
,A=30°,则角C等于