题目内容
如果函数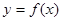 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。
(1)判断函数 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;
(2)已知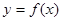 具有“
具有“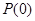 性质”,且当
性质”,且当 时
时 ,求
,求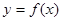 在
在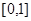 上有最大值;
上有最大值;
(3)设函数 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若 与
与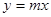 交点个数为2013,求
交点个数为2013,求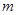 的值.
的值.
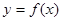 的定义域为R,对于定义域内的任意
的定义域为R,对于定义域内的任意 ,存在实数
,存在实数 使得
使得 成立,则称此函数具有“
成立,则称此函数具有“ 性质”。
性质”。(1)判断函数
 是否具有“
是否具有“ 性质”,若具有“
性质”,若具有“ 性质”,求出所有
性质”,求出所有 的值;若不具有“
的值;若不具有“ 性质”,说明理由;
性质”,说明理由;(2)已知
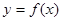 具有“
具有“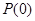 性质”,且当
性质”,且当 时
时 ,求
,求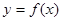 在
在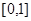 上有最大值;
上有最大值;(3)设函数
 具有“
具有“ 性质”,且当
性质”,且当 时,
时, .若
.若 与
与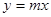 交点个数为2013,求
交点个数为2013,求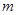 的值.
的值.(1) 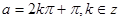 ,(2) 当
,(2) 当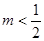 时,
时,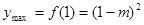 ,当
,当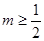 时,
时,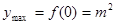 , (3)
, (3) 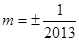 .
.
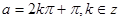 ,(2) 当
,(2) 当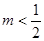 时,
时,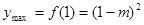 ,当
,当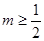 时,
时,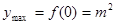 , (3)
, (3) 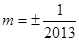 .
.试题分析:(1)新定义问题,必须从定义出发,实际是对定义条件的直译. 由
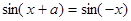 得
得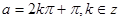 ,(2)由
,(2)由 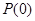 性质知函数为偶函数. ∴
性质知函数为偶函数. ∴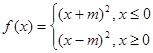 当
当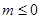 时,∵
时,∵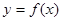 在
在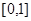 单调增,∴
单调增,∴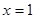 时,
时,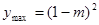 ,当
,当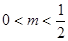 时,∵
时,∵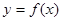 在
在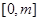 单调减,在
单调减,在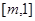 上单调增,又
上单调增,又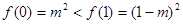 ,∴
,∴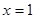 时,
时,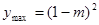 ,当
,当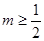 时,∵
时,∵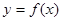 在
在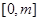 单调减,在
单调减,在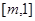 上单调增,又
上单调增,又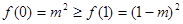 ,∴
,∴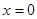 时,
时,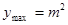 . (3) ∵函数
. (3) ∵函数 具有“
具有“ 性质” ∴
性质” ∴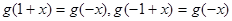 ∴
∴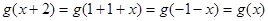 ∴函数
∴函数 是以2为周期的函数. 当
是以2为周期的函数. 当 时,
时, 为偶函数,因此易得函数
为偶函数,因此易得函数 是以1为周期的函数.结合图像得: ①当
是以1为周期的函数.结合图像得: ①当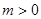 时,要使得
时,要使得 与
与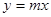 有2013个交点,只要
有2013个交点,只要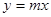 与
与 在区间
在区间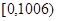 有2012个交点,而在
有2012个交点,而在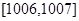 内有一个交点∴
内有一个交点∴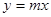 过
过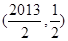 ,从而得
,从而得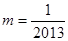 ,②当
,②当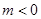 时,同理可得
时,同理可得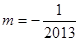 ,③当
,③当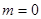 时,不合题意, 综上所述
时,不合题意, 综上所述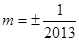 .
.(1)由
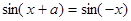 得
得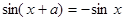
∴
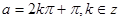
∴函数
 具有“
具有“ 性质”,其中
性质”,其中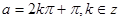 2分
2分(2) ∵
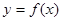 具有“
具有“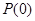 性质”
性质”∴
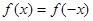
设
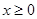 ,则
,则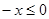 ,∴
,∴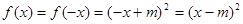
∴
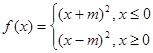 4分
4分当
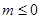 时,∵
时,∵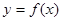 在
在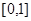 单调增,∴
单调增,∴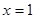 时,
时,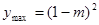 5分
5分当
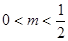 时,∵
时,∵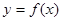 在
在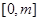 单调减,在
单调减,在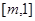 上单调增
上单调增又
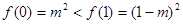 ,∴
,∴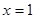 时,
时,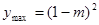 6分
6分当
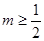 时,∵
时,∵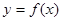 在
在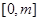 单调减,在
单调减,在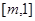 上单调增
上单调增又
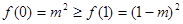 ,∴
,∴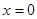 时,
时,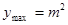 7分
7分综上得当
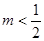 时,
时,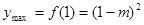 ,当
,当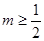 时,
时,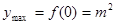 8分
8分(3) ∵函数
 具有“
具有“ 性质”
性质” ∴
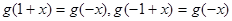
∴
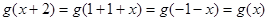 ,
,∴函数
 是以2为周期的函数 9分
是以2为周期的函数 9分设
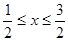 ,则
,则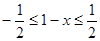 ,
,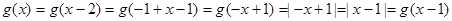
再设
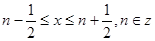
当
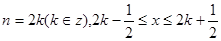 ,则
,则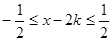
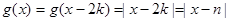
当
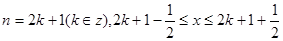 ,则
,则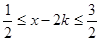
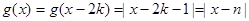
∴对于
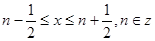 ,都有
,都有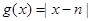
而
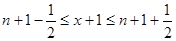
∴
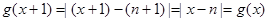
∴函数
 是以1为周期的函数 12分
是以1为周期的函数 12分①当
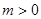 时,要使得
时,要使得 与
与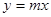 有2013个交点,只要
有2013个交点,只要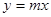 与
与 在区间
在区间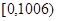 有2012个交点,而在
有2012个交点,而在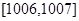 内有一个交点
内有一个交点∴
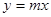 过
过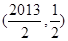 ,从而得
,从而得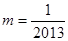 14分
14分②当
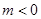 时,同理可得
时,同理可得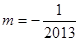
③当
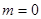 时,不合题意
时,不合题意综上所述
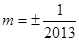 16分
16分
练习册系列答案
相关题目
 在
在 处取得最大值,则
处取得最大值,则



 ,则a=( )
,则a=( )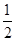 x2+bln(x+2)在(-1,+∞)上是减函数,则b的取值范围是( )
x2+bln(x+2)在(-1,+∞)上是减函数,则b的取值范围是( ) 的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是( )
的单位:s,v的单位:m/s)行驶至停止,在此期间汽车继续行驶的距离(单位:m)是( )
 ,若
,若 ,
,

 ,则
,则 ( )
( ) 值变化
值变化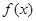 满足
满足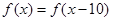 ,当
,当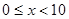 时,
时,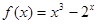 ,则函数
,则函数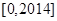 上的零点个数为( )
上的零点个数为( ) 存在零点,且对任意
存在零点,且对任意 都满足
都满足 若关于
若关于 的方程
的方程 恰有三个不同的根,则实数
恰有三个不同的根,则实数 的取值范围是
的取值范围是
 与
与 ,若
,若 与
与 的交点在直线
的交点在直线 的两侧,
的两侧, 的取值范围是 ( )
的取值范围是 ( )


