题目内容
若函数f(x)=
-k只有一个零点,则实数k=
| 1 | |x|-1 |
-1
-1
.分析:由题意可得,方程
=k只有一个实数根,函数y=
的图象和直线 y=k只有一个交点,数形结合可得k的值.
| 1 |
| |x|-1 |
| 1 |
| |x|-1 |
解答: 解:∵函数f(x)=
解:∵函数f(x)=
-k只有一个零点,
∴方程
=k只有一个实数根,
∴函数y=
=
的图象和直线 y=k只有一个交点,
画出函数y=
的图象的单调性示意图,数形结合可得k=-1,
故答案为:-1.
 解:∵函数f(x)=
解:∵函数f(x)=| 1 |
| |x|-1 |
∴方程
| 1 |
| |x|-1 |
∴函数y=
| 1 |
| |x|-1 |
|
画出函数y=
| 1 |
| |x|-1 |
故答案为:-1.
点评:本题主要考查函数的零点与方程的根的关系,体现了转化以及数形结合的数学学思想,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
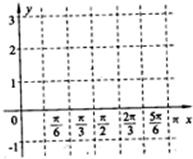 设函数f(x)=
设函数f(x)=