Question

设函数f（x）=

a

• 

b

，其中向量

a

=（2cosx，1），

b

=（cosx，

3

sin2x），x∈R．
（1）若函数f（x）=1-

3

，且x∈[-

π

3

，

π

3

]，求x；
（2）求函数y=f（x）的单调增区间；
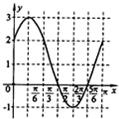
并在给出的坐标系中画出y=f（x）在区间[0，π]上的图象．

Answer 1

分析：（1）化简函数的解析式为 f（x）=2sin（2x+

π

6

 ）+1，由f（x）=1-

3

，解得sin（2x+

π

6

 ）=-

3

2

，结合x的
范围，求出x值．
（2）由 2kπ-

π

2

≤2x+

π

6

≤2kπ+

π

2

，k∈z，求得x的范围即得单调增区间，有五点法做出其图象．

解答：解：（1）依题设得函数f（x）=2cos²x+

3

sin2x=1+2cos2x+

3

sin2x=2sin（2x+

π

6

 ）+1，
由 2sin（2x+

π

6

 ）=1=1-

3

，∴sin（2x+

π

6

 ）=-

3

2

．∵-

π

3

≤x≤

π

3

，
∴-

π

2

≤2x+

π

6

≤

5π

6

，∴2x+

π

6

=-

π

3

，x=-

π

4

．
（2）由 2kπ-

π

2

≤2x+

π

6

≤2kπ+

π

2

，k∈z，得 kπ-

π

3

≤x≤kπ+

π

6

，
得函数单调增区间为[kπ-

π

3

，kπ+

π

6

]．

x	0	π 6	π 3	π 2	2π 3	5π 6	π
y	2	3	2	0	-1	0	2

点评：本题考查两个向量的数量积公式的应用，正弦函数的单调性，以及用五点法作y=Asin（ωx+∅）的简图，化简函数
f（x）的解析式是解题的突破口．