题目内容
设△ABC的内角A、B、C所对的边长分别为a、b、c,且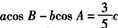 。
。
(1)求tanAcotB的值;
(2)求tan(A-B)的最大值。
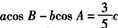 。
。(1)求tanAcotB的值;
(2)求tan(A-B)的最大值。
解:(1)由正弦定理得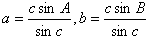
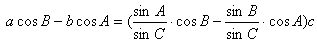
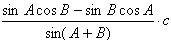
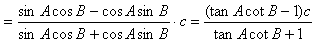
依题设得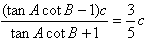
解得tanAcotB=4;
(2)由(1)得tanA=4tanB,故A、B都是锐角,于是tanB>0
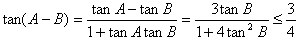
且当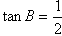 时,上式取等号
时,上式取等号
因此tan(A-B)的最大值为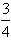 。
。
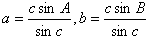
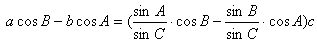
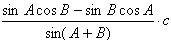
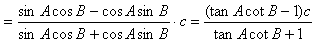
依题设得
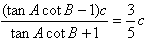
解得tanAcotB=4;
(2)由(1)得tanA=4tanB,故A、B都是锐角,于是tanB>0
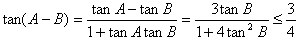
且当
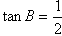 时,上式取等号
时,上式取等号因此tan(A-B)的最大值为
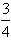 。
。
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目