Question

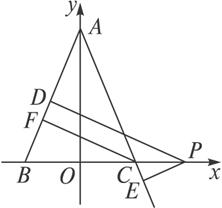
用解析法证明：等边三角形内一点到三边距离之和为定值．

Answer 1

分析：先设等边三角形的边长为2a，以BC所在的直线为x轴，以BC的垂直平分线为y轴建立平面直角坐标系，可得B（-a，0），C（a，0），
A（0，

3

），即可得到直线AB，直线AC及直线BC的方程，设三角形内任一点P（m，n），利用点到直线的距离公式求出P到三边的距离之和得到为定值即可．

解答：解：先设等边三角形的边长为2a，以BC所在的直线为x轴，
以BC的垂直平分线为y轴建立平面直角坐标系，
可得B（-a，0），C（a，0），
A（0，

3

）设三角形内任一点P（m，n），
且直线AB的斜率为k=tan60°=

3

，
所以AB的方程为：y-0=

3

（x+a），化简得

3

x-y+

3

a=0；
直线BC的方程为y=0；直线AC的斜率为k′=tan120°=-

3

，
所以直线AC的方程为：y-0=-

3

（x-a），
化简得：

3

x+y-

3

a=0；
所以利用点到直线的距离公式得到P到三边的距离和=PE+PF+PD=|

3 m-n+ 3 a

2

|+|

3 m+n- 3 a

2

|+|n|=

3

a，
故得证．

点评：考查学生灵活运用点到直线的距离公式的能力，以及会求直线解析式的能力．