Question

用解析法证明:等腰三角形底边延长线上一点到两腰的距离之差等于一腰上的高.

Answer 1

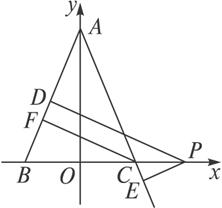
在△ABC中,AB=AC,P为BC延长线上一点,

PD⊥AB于D,PE⊥AC于E,CF⊥AB于F.

以BC所在直线为x轴,以BC中垂线为y轴,

建立直角坐标系(如图3-3-1).

设A(0,b),B(-a,0),C(a,0),(a＞0,b＞0),

则直线AB的方程为bx-ay+ab=0,直线AC的方程为bx+ay-ab=0,

取P(x₀,0),使x₀＞a,

则点P到直线AB,AC的距离分别为

|PD|=,

|PE|=.

点C到直线AB的距离为

|CF|=,

则|PD|-|PE|==|CF|.

解析:

根据图形的特点,建立适当直角坐标系,利用坐标解决有关问题,这种方法叫坐标法,也称为解析法.