题目内容
函数 为f(x)的导函数,令
为f(x)的导函数,令 则下列关系正确的是
则下列关系正确的是
- A.f(a)>f(b)
- B.f(a)<f(b)
- C.f(a)=f(b)
- D.f(|a|)>f(b)
A
分析:先求出f′(x),然后令x= 即可求出f′(
即可求出f′( ),确定出f(x)的解析式,由cosx的值域得到f′(x)=cosx-1下于等于0,即可得到f(x)为递减函数,则由a小于b,得到f(a)大于f(b)即可.
),确定出f(x)的解析式,由cosx的值域得到f′(x)=cosx-1下于等于0,即可得到f(x)为递减函数,则由a小于b,得到f(a)大于f(b)即可.
解答:因为f′(x)=cosx+2f′( ),
),
所以f′( )=cos
)=cos +2f′(
+2f′( ),解得f′(
),解得f′( )=-
)=-
所以f(x)=sinx-x,由f′(x)=cosx-1≤0,得到f(x)为递减函数,
而- <log32,则f(-
<log32,则f(- )>f(log32)即f(a)>f(b).
)>f(log32)即f(a)>f(b).
故选A
点评:本题是一道综合题,学生做题时注意f′( )应为常数项,突破点是求出导函数后令x=
)应为常数项,突破点是求出导函数后令x= .此题要求学生掌握导数的运算法则.
.此题要求学生掌握导数的运算法则.
分析:先求出f′(x),然后令x=
 即可求出f′(
即可求出f′( ),确定出f(x)的解析式,由cosx的值域得到f′(x)=cosx-1下于等于0,即可得到f(x)为递减函数,则由a小于b,得到f(a)大于f(b)即可.
),确定出f(x)的解析式,由cosx的值域得到f′(x)=cosx-1下于等于0,即可得到f(x)为递减函数,则由a小于b,得到f(a)大于f(b)即可.解答:因为f′(x)=cosx+2f′(
 ),
),所以f′(
 )=cos
)=cos +2f′(
+2f′( ),解得f′(
),解得f′( )=-
)=-
所以f(x)=sinx-x,由f′(x)=cosx-1≤0,得到f(x)为递减函数,
而-
 <log32,则f(-
<log32,则f(- )>f(log32)即f(a)>f(b).
)>f(log32)即f(a)>f(b).故选A
点评:本题是一道综合题,学生做题时注意f′(
 )应为常数项,突破点是求出导函数后令x=
)应为常数项,突破点是求出导函数后令x= .此题要求学生掌握导数的运算法则.
.此题要求学生掌握导数的运算法则. 
练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
已知函数f(x)的定义域为[-3,+∞),部分函数值如表所示,其导函数的图象如图所示,若正数a,b满足f(2a+b)<1,则
的取值范围是( )

| b+2 |
| a+2 |

A、(
| ||
B、(
| ||
| C、(1,4) | ||
D、(-∞,
|
 已知函数f(x)的定义域为[-2,+∞),部分函数值如下表,f'(x)为f(x)的导函数,f'(x)的图象如图所示.如果实数a满足f(a)<1,则a的取值范围是( ) 已知函数f(x)的定义域为[-2,+∞),部分函数值如下表,f'(x)为f(x)的导函数,f'(x)的图象如图所示.如果实数a满足f(a)<1,则a的取值范围是( )
|
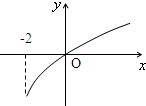 已知函数f(x)的定义域为[-2,+∞),部分函数值如下表,f'(x)为f(x)的导函数,f'(x)的图象如图所示.如果实数a满足f(a)<1,则a的取值范围是
已知函数f(x)的定义域为[-2,+∞),部分函数值如下表,f'(x)为f(x)的导函数,f'(x)的图象如图所示.如果实数a满足f(a)<1,则a的取值范围是
| x | -2 | 0 | 4 |
| f(x) | 1 | -1 | 1 |
- A.(-2,0)
- B.(0,4)
- C.(-2,4)
- D.[-2,4)
 已知函数f(x)的定义域为[-3,+∞),部分函数值如表所示,其导函数的图象如图所示,若正数a,b满足f(2a+b)<1,则
已知函数f(x)的定义域为[-3,+∞),部分函数值如表所示,其导函数的图象如图所示,若正数a,b满足f(2a+b)<1,则