题目内容
两人进行乒乓球比赛,先赢三局者获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有
- A.10种
- B.15种
- C.20种
- D.30种
C
分析:根据分类计数原理,所有可能情形可分为三类,在每一类中可利用组合数公式计数,最后三类求和即可得结果
解答:第一类:三局为止,共有2种情形;
第二类:四局为止,共有2×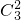 =6种情形;
=6种情形;
第三类:五局为止,共有2× =12种情形;
=12种情形;
故所有可能出现的情形共有2+6+12=20种情形
故选C
点评:本题主要考查了分类和分步计数原理的运用,组合数公式的运用,分类讨论的思想方法,属基础题
分析:根据分类计数原理,所有可能情形可分为三类,在每一类中可利用组合数公式计数,最后三类求和即可得结果
解答:第一类:三局为止,共有2种情形;
第二类:四局为止,共有2×
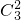 =6种情形;
=6种情形;第三类:五局为止,共有2×
 =12种情形;
=12种情形;故所有可能出现的情形共有2+6+12=20种情形
故选C
点评:本题主要考查了分类和分步计数原理的运用,组合数公式的运用,分类讨论的思想方法,属基础题

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目