题目内容
设函数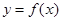 在区间(
在区间(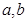 )的导函数
)的导函数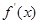 ,
,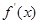 在区间(
在区间(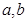 )的导函数
)的导函数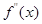 ,若在区间(
,若在区间(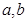 )上
)上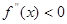 恒成立,则称函数
恒成立,则称函数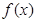 在区间(
在区间(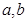 )为凸函数,已知
)为凸函数,已知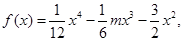 若当实数
若当实数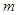 满足
满足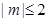 时,函数
时,函数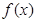 在
在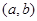 上为凸函数,则
上为凸函数,则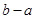 最大值 ( )
最大值 ( )
A.1 B.2 C.3 D.4
【答案】
D
【解析】
试题分析:
 ,
, ,函数
,函数 在
在 上为凸函数,
上为凸函数, 对于
对于 恒成立,
恒成立,
设函数 与x轴交点横坐标为
与x轴交点横坐标为 ,
, 的最大值为
的最大值为

 最大值为4
最大值为4
考点:信息题及函数图像及性质
点评:本题根据题目中凸函数的定义可知对于函数 满足性质
满足性质 对于
对于 恒成立,进而结合二次函数性质求得
恒成立,进而结合二次函数性质求得 最大值
最大值

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
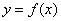 在区间(
在区间(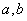 )的导函数
)的导函数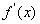 ,
,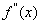 ,若在区间(
,若在区间(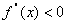 恒成立,则称函数
恒成立,则称函数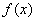 在区间(
在区间(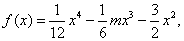 若当实数
若当实数 满足
满足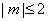 时,函数
时,函数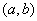 上为凸函数,则
上为凸函数,则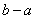 最大值是_________.
最大值是_________.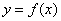 在区间(
在区间(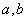 )的导函数
)的导函数 ,
,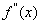 ,若在区间(
,若在区间( 恒成立,则称函数
恒成立,则称函数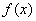 在区间(
在区间(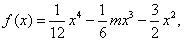 若当实数
若当实数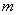 满足
满足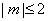 时,函数
时,函数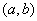 上为凸函数,则
上为凸函数,则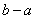 最大值是_________.
最大值是_________.