题目内容
设函数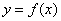 在区间(
在区间(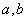 )的导函数
)的导函数 ,
, 在区间(
在区间(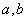 )的导函数
)的导函数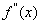 ,若在区间(
,若在区间(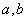 )上
)上 恒成立,则称函数
恒成立,则称函数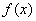 在区间(
在区间(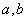 )为凸函数,已知
)为凸函数,已知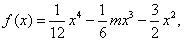 若当实数
若当实数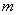 满足
满足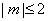 时,函数
时,函数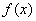 在
在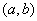 上为凸函数,则
上为凸函数,则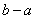 最大值是_________.
最大值是_________.
【答案】
4
【解析】
试题分析:
设 与x轴交点为
与x轴交点为


 最大值为4
最大值为4
考点:函数导数与单调性
点评:求解本题首先要根据题目中给定的凸函数的定义将函数 二次求导,求得其单调区间且满足
二次求导,求得其单调区间且满足 是减区间的子区间
是减区间的子区间

练习册系列答案
相关题目
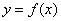 在区间(
在区间(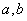 )的导函数
)的导函数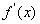 ,
,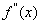 ,若在区间(
,若在区间(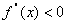 恒成立,则称函数
恒成立,则称函数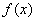 在区间(
在区间(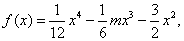 若当实数
若当实数 满足
满足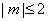 时,函数
时,函数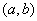 上为凸函数,则
上为凸函数,则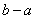 最大值是_________.
最大值是_________.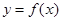 在区间(
在区间(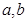 )的导函数
)的导函数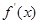 ,
,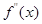 ,若在区间(
,若在区间(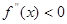 恒成立,则称函数
恒成立,则称函数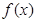 在区间(
在区间(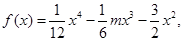 若当实数
若当实数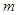 满足
满足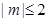 时,函数
时,函数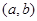 上为凸函数,则
上为凸函数,则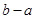 最大值 ( )
最大值 ( )