Question

已知椭圆的中心在原点，离心率为，一个焦点是F(-m,0)(m是大于0的常数).

(1)求椭圆的方程；

(2)设Q是椭圆上的一点，且过点F、Q的直线l与y轴交于点M.若||=2||，求直线l的斜率.

Answer 1

思路分析：本题主要考查直线、椭圆和向量等基本知识，以及推理能力和运算能力.

(1)根据题目所描述的椭圆的性质求出椭圆方程；

(2)将||=2||转化为定比分点问题，分两种情况求斜率.

解：(1)设所求椭圆方程是=1(a＞b＞0).由已知，得c=m,=,所以a=2m,b=m.故所求的椭圆方程是=1.

(2)设Q(x_Q,y_Q),直线l：y=k(x+m),则点M(0，km).

当=2时，由于F(-m,0),M(0,km),由定比分点坐标公式，得x_Q=

又点Q(-)在椭圆上，所以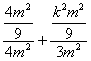=1.解得k=±2.

当=-2时，x_Q==-2m,y_Q==-km.

于是=1,解得k=0.故直线l的斜率是0，±2.

温馨提示

(1)根据条件椭圆方程是何种形式，用待定系数法求椭圆方程，关键是判定焦点在哪一条轴上；(2)将向量模的关系转化为定比分点问题是解这一问的关键.