Question

如图，在平面直角坐标系中，点，直线．设圆的半径为，圆心在上．
（1）若圆心也在直线上，过点作圆的切线，求切线的方程；
（2）若圆上存在点，使，求圆心的横坐标的取值范围．

Answer 1

（1）y=0或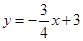；（2）0≤a≤．

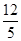解析试题分析：（1）先求出圆心坐标，可得圆的方程，再设出切线方程，利用点到直线的距离公式，即可求得切线方程；（2）设出点C，M的坐标，利用MA=2MO，寻找坐标之间的关系，进一步将问题转化为圆与圆的位置关系，即可得出结论．
解：（1）联立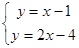：，得圆心为：C(3，2)．
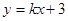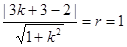设切线为：，d＝，得：．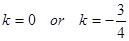
故所求切线为：．                    5′
（2）设点M(x，y)，由，知：，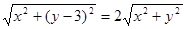
化简得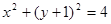：，即：点M的轨迹为以(0，1)为圆心，2为半径的圆，可记为圆D．
又因为点在圆上，故圆C圆D的关系为相交或相切．
故：1≤|CD|≤3，其中．
解之得：0≤a≤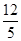．                             5′
考点：直线和圆的方程的应用．