题目内容
已知动圆 (
( )
)
(1)当 时,求经过原点且与圆
时,求经过原点且与圆 相切的直线
相切的直线 的方程;
的方程;
(2)若圆 恰在圆
恰在圆 的内部,求实数
的内部,求实数 的取值范围.
的取值范围.
(1)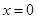 或
或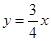 (2)
(2)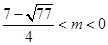 或
或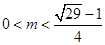
解析试题分析:(1) 时,
时,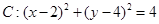 。圆心为
。圆心为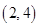 半径为2。讨论直线
半径为2。讨论直线 的斜率是否存在,根据直线与圆相切时圆心到直线的距离等于半径,可得直线
的斜率是否存在,根据直线与圆相切时圆心到直线的距离等于半径,可得直线 的方程。(2)圆
的方程。(2)圆 的圆心
的圆心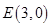 ,半径为4。圆
,半径为4。圆 的圆心
的圆心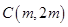 ,半径为
,半径为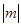 ,圆
,圆 在圆
在圆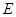 的内部,等价于圆
的内部,等价于圆 内含于圆
内含于圆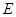 即
即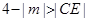 ,注意讨论
,注意讨论 的正负去绝对值,从而可解得
的正负去绝对值,从而可解得 的范围。
的范围。
(1)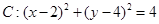
当直线 的斜率不存在时,
的斜率不存在时, 方程为
方程为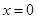 ,(3分)
,(3分)
当直线 的斜率存在时,设
的斜率存在时,设 方程为
方程为 ,由题意得
,由题意得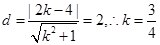
所以 方程为
方程为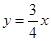 (6分)
(6分)
(2)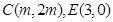 ,由题意得
,由题意得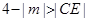 ,
,
得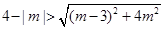 (9分)
(9分)
当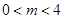 时,解得
时,解得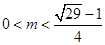 ,
,
当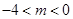 时,解得
时,解得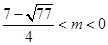
考点:1直线与圆的位置关系;2两圆位置关系。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,圆
,圆 .
. 被圆
被圆 所截得的弦长;
所截得的弦长; 的直线
的直线 与直线
与直线 垂直,
垂直, 上的圆
上的圆 相切,圆
相切,圆 ,求圆
,求圆 中,点
中,点 ,直线
,直线 .设圆
.设圆 的半径为
的半径为 ,圆心在
,圆心在 上.
上. 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围.
的取值范围.
 ,求圆C方程.
,求圆C方程.
 +y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.
+y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点. ,则
,则 (O为坐标原点)等于
(O为坐标原点)等于