题目内容
已知实数 .
.
(1)求直线y=ax+b不经过第四象限的概率:
(2)求直线y=ax+b与圆 有公共点的概率.
有公共点的概率.
(1) ;(2)
;(2)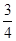 .
.
解析试题分析:(1)因为实数 ,所以由
,所以由 构成的实数对总共有16种,又直线
构成的实数对总共有16种,又直线 不过第四象限,即必须满足
不过第四象限,即必须满足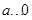 且
且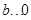 ,此时由
,此时由 构成的实数对总共有4种,故所求概率为
构成的实数对总共有4种,故所求概率为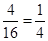 ;(2)由圆方程
;(2)由圆方程 知圆心坐标为
知圆心坐标为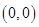 ,半径为1,又直线与圆有公共点,即圆心到直线的距离
,半径为1,又直线与圆有公共点,即圆心到直线的距离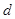 不大于半径1,根据点到直线距离公式得
不大于半径1,根据点到直线距离公式得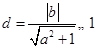 ,整理得
,整理得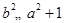 ,经检验满足此式的
,经检验满足此式的 实数对共有12种,故所求概率为
实数对共有12种,故所求概率为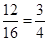 .
.
(1)由于实数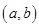 的所有取值为:
的所有取值为: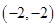 ,
,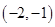 ,
,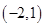 ,
,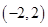 ,
,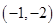 ,
,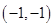 ,
,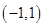 ,
,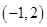 ,
,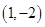 ,
,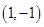 ,
,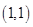 ,
,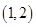 ,
,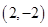 ,
,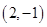 ,
,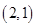 ,
,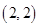 共16种. 2分
共16种. 2分
设“直线 不经过第四象限”为事件
不经过第四象限”为事件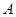 ,若直线
,若直线 不经过第四象限,则必须满足
不经过第四象限,则必须满足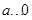 ,
,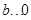 .
.
则事件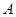 包含4个基本事件:
包含4个基本事件: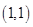 ,
,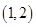 ,
,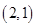 ,
,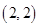 . 4分
. 4分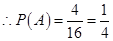 ,直线
,直线 不经过第四象限的概率为
不经过第四象限的概率为 . 6分
. 6分
(2)设“直线 与圆
与圆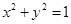 有公共点”为事件
有公共点”为事件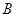 ,
,
则需满足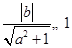 ,即
,即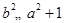 . 9分
. 9分
所以事件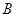 包含12个基本事件:
包含12个基本事件: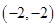 ,
,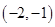 ,
,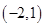 ,
,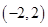 ,
,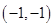 ,
,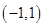 ,
,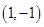 ,
,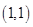 ,
,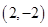 ,
,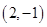 ,
,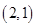 ,
,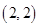 . 11分
. 11分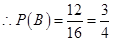 ,所以直线
,所以直线 与圆
与圆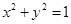 有公共点的概率为
有公共点的概率为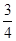 . 13分
. 13分
考点:1.古典概型;2.直线与圆.

练习册系列答案
相关题目
 中,曲线
中,曲线 的参数方程为
的参数方程为 ,(其中
,(其中 为参数,
为参数, ),在极坐标系(以坐标原点
),在极坐标系(以坐标原点 为极点,以
为极点,以 轴非负半轴为极轴)中,曲线
轴非负半轴为极轴)中,曲线 的极坐标方程为
的极坐标方程为 .
. 和
和 ,求曲线
,求曲线 (
( )
) 时,求经过原点且与圆
时,求经过原点且与圆 相切的直线
相切的直线 的方程;
的方程; 内切,求实数
内切,求实数 的值.
的值. 中,点
中,点 ,直线
,直线 .设圆
.设圆 的半径为
的半径为 ,圆心在
,圆心在 上.
上. 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围.
的取值范围.

 为何值时,曲线C表示圆;
为何值时,曲线C表示圆; 交于M、N两点,且
交于M、N两点,且 ,求
,求 与圆
与圆 交于
交于 ,
, 两点,是否存在实数
两点,是否存在实数 为直径的圆过原点,若存在,求出实数
为直径的圆过原点,若存在,求出实数
 有公共点,则直线l的斜率的取值范围为________.
有公共点,则直线l的斜率的取值范围为________.