题目内容
一动圆与圆x2+y2+6x+5=0外切,同时与圆x2+y2-6x-91=0内切,
求动圆圆心M的轨迹方程,并说明它是什么曲线.
解 如图所示,设动圆圆心为M(x,y),半径为R,设已知圆的圆心分别为O1,O2,将圆的方程分别配方得(x+3)2+y2=4,(x-3)2+y2=100,
当动圆与圆O1相外切时,
有|O1M|=R+2.①
当动圆与圆O2相内切时,有|O2M|=10-R.②
将①②两式相加,得|O1M|+|O2M|=12>|O1O2|,
∴动圆圆心M(x,y)到点O1(-3,0)和O2(3,0)的距离和是常数12,
所以点M的轨迹是焦点为O1(-3,0),O2(3,0),
长轴长等于12的椭圆.
∴2c=6,2a=12,∴c=3,a=6,∴b2=36-9=27,
∴圆心轨迹方程为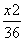 +
+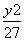 =1,轨迹为椭圆.
=1,轨迹为椭圆.

练习册系列答案
相关题目
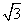 x与双曲线C:
x与双曲线C: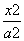 -
-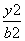 =1(a>0,b>0)左右两支分别交于M、N两点,F是双曲线C的右焦点,O是坐标原点,若|FO|=|MO|,则双曲线的离心率等于( ).
=1(a>0,b>0)左右两支分别交于M、N两点,F是双曲线C的右焦点,O是坐标原点,若|FO|=|MO|,则双曲线的离心率等于( ).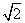 B.
B.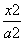 -
-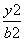 =1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为
=1(a>0,b>0)的两条渐近线与抛物线y2=2px(p>0)的准线分别交于A,B两点,O为坐标原点.若双曲线的离心率为2,△AOB的面积为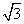 ,则p=( ).
,则p=( ).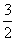 C.2 D.3
C.2 D.3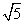 C.2 D.
C.2 D.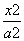 +
+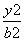 =1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为 ( ).
=1(a>b>0)的右焦点为F(3,0),过点F的直线交E于A,B两点.若AB的中点坐标为(1,-1),则E的方程为 ( ).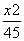 +
+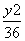 =1 B.
=1 B.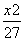 +
+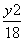 =1 D.
=1 D.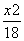 +
+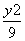 =1
=1 -
-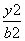 =1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( ).
=1(a>0,b>0)有相同的焦点F,点A是两曲线的交点,且AF⊥x轴,则双曲线的离心率为( ).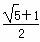 B.
B. +1 C.
+1 C. +1 D.
+1 D. 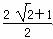
 ”的单调递增函数是( )
”的单调递增函数是( ) (B)
(B) (C)
(C)
 1/2 (D)
1/2 (D)