题目内容
17.已知圆C的圆心是直线x-y+1=0与y轴的交点,且圆C与直线x+y+3=0相切,则圆的标准方程为( )| A. | x2+(y-1)2=8 | B. | x2+(y+1)2=8 | C. | (x-1)2+(y+1)2=8 | D. | (x+1)2+(y-1)2=8 |
分析 对于直线x-y+1=0,令x=0,解得y.可得圆心C.设圆的半径为r,利用点到直线的距离公式及其圆C与直线x+y+3=0相切的充要条件可得r.
解答 解:对于直线x-y+1=0,令x=0,解得y=1.
∴圆心C(0,1),
设圆的半径为r,
∵圆C与直线x+y+3=0相切,
∴r=$\frac{|1+3|}{\sqrt{2}}$=2$\sqrt{2}$,
∴圆的标准方程为x2+(y-1)2=8.
故选:A.
点评 本题考查了点到直线的距离公式及其圆与直线相切的充要条件,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7.在如图所示的程序框图中,输入A=22,B=4,则输出的结果是( )


| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
8.复数$\frac{i}{1+i}$-$\frac{1}{2i}$的实部与虚部的和为( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
9.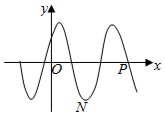 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
 已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )
已知函数$f(x)=Acos(wx+φ)(w>0,|φ|<\frac{π}{2})$的部分图象如图所示,其中N,P的坐标分别为$(\frac{5}{8}π,-A),(\frac{11}{8}π,-0)$,则函数f(x)的单调递减区间不可能为( )| A. | $[\frac{π}{8},\frac{5π}{8}]$ | B. | $[-\frac{7π}{8},-\frac{3π}{8}]$ | C. | $[\frac{9π}{4},\frac{21π}{8}]$ | D. | $[\frac{9π}{8},\frac{33π}{8}]$ |