题目内容
【题目】等比数列
满足：
，且
，
，
成等差数列.
（1）求数列的通项公式；
（2）若不等式
成立的正整数
恰有4个，求正整数
的值.
【答案】（1）
；（2）
.
【解析】
（1）利用等比数列的通项公式计算即可；
（2）结合条件对n进行分类讨论，当
时利用分离常数法化简得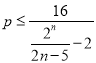
，利用取特值和做商法判断出
的单调性，再判断出
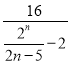的单调性，根据条件即可求出正整数p的值．
（1）已知等比数列
满足：
，设公比为
，且
，
，
成等差数列，
∴
，得
，解得
，或
（舍）.
所以
，即；
（2）由（1）得，
，
∵
，∴当n＝1、2时，上式一定成立；
当时，化简
＝，
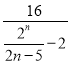当n＝3时，
＝
＝
，
当n＝4时，
＝
＝4.8，
当n＝5时，
＝
，
当n＝6时，
，…
设bn＝，则
＝
＝
＝2（1﹣
），
当n≥4时，2（1﹣）≥
，则＞1，
∴当n≥4时，bn随着n的增大而增大，则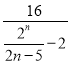随着n的增大而减小，
∵不等式
成立的正整数
恰有4个，即n＝1、2、4、5，
∴正整数
的值为3．
练习册系列答案
相关题目
