题目内容
已知函数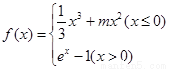
(1)讨论函数f (x)的极值情况;
(2)设g (x) = ln (x + 1),当x1>x2>0时,试比较f (x1 – x2)与g (x1 – x2)及g (x1) –g (x2)三者的大小;并说明理由.(参考公式: 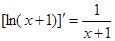 )
)
(1)f (x)有极小值f (0) = 0,f (x)有极大值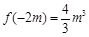
(2)f (x1 – x2)> g (x1 – x2) > g (x1) –g (x2)
【解析】(1)当x>0时,f (x) = ex – 1在(0,+∞)单调递增,且f (x)>0;
当x≤0时,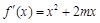 .
.
①若m = 0,f ′(x)
= x2≥0, f (x) =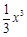 在(–∞,0]上单调递增,且f (x) =
在(–∞,0]上单调递增,且f (x) =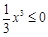 .
.
又f (0) = 0,∴f (x)在R上是增函数,无极植;
②若m<0,f ′(x)
= x(x + 2m) >0,则f (x) =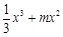 在(–∞,0)单调递增,同①可知f (x)在R上也是增函数,无极值;…………………………………………4分
在(–∞,0)单调递增,同①可知f (x)在R上也是增函数,无极值;…………………………………………4分
③若m>0,f (x)在(–∞,–2m]上单调递增,在(–2m,0)单调递减,
又f (x)在(0, +∞)上递增,故f (x)有极小值f (0) = 0,f (x)有极大值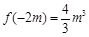 . 6分
. 6分
(2)当x >0时,先比较ex – 1与ln(x + 1)的大小,
设h(x) = ex – 1–ln(x + 1) (x
>0) ∴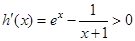 恒成立
恒成立
∴h(x)在(0,+∞)是增函数,h(x)>h (0) = 0
∴ex – 1–ln(x + 1) >0即ex – 1>ln(x + 1) 也就是f (x) > g (x) , 成立.
成立.
故当x1 – x2>0时,f (x1 – x2)> g (x1 – x2)……………………10分
再比较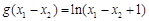 与g (x1) –g (x2)
= ln(x1 + 1) –ln(x2 + 1)的大小.
与g (x1) –g (x2)
= ln(x1 + 1) –ln(x2 + 1)的大小.
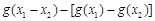 =
=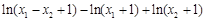
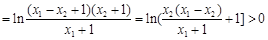 ∴g (x1 – x2) > g (x1)
–g (x2)
∴g (x1 – x2) > g (x1)
–g (x2)
∴f (x1 – x2)> g (x1 – x2) > g (x1) –g (x2) .…………………14分

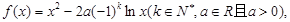
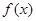 的单调性;
的单调性;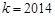 时,关于
时,关于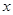 的方程
的方程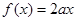 有唯一解,求
有唯一解,求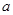 的值;
的值;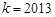 时,证明: 对一切
时,证明: 对一切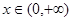 ,都有
,都有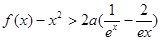 成立.
成立.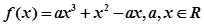
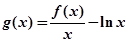 的单调区间;
的单调区间;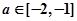 ,使函数
,使函数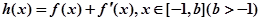 在
在 处取得最小值,试求
处取得最小值,试求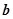 的最大值.
的最大值. 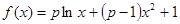 .
.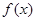 的单调性;
的单调性;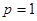 时,
时,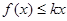 恒成立,求实数
恒成立,求实数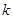 的取值范围;
的取值范围;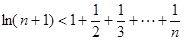
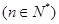 .
.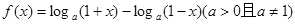
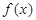 的奇偶性与单调性;
的奇偶性与单调性;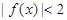 的解集为
的解集为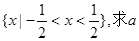 的值;
的值;