题目内容
(本小题满分12分)已知函数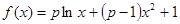 .
.
(1)讨论函数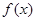 的单调性;
的单调性;
(2)当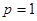 时,
时,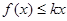 恒成立,求实数
恒成立,求实数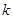 的取值范围;
的取值范围;
(3)证明: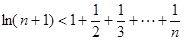
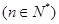 .
.
【答案】
(1)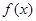 在
在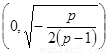 单调递增,在
单调递增,在 单调递减.(2)
单调递减.(2)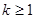 ;(3)见解析.
;(3)见解析.
【解析】本试题主要考查了导数在研究函数中的运用。那么利用先求函数定义域,然后求解导数,根据导数的正负判定函数的单调性
第二问中,当p=1时,f(x)《kx恒成立等价于1+lnx《kx,然后分离参数的思想得到k》(1+lnx)/x,构造函数得到参数k的范围。
第三问中,要证明不等式成立,则需要分析由(2)知当k=1时,有f(x)《x,当x>>1时,f(x)《x即lnx<x-1,结合放缩法得到证明。
解:(1)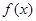 的定义域为(0,+∞),
的定义域为(0,+∞),
当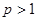 时,
时,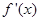 >0,故
>0,故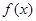 在(0,+∞)单调递增;
在(0,+∞)单调递增;
当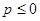 时,
时,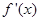 <0,故
<0,故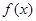 在(0,+∞)单调递减;……………2分
在(0,+∞)单调递减;……………2分
当-1<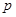 <0时,令
<0时,令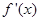 =0,解得
=0,解得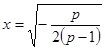 .
.
则当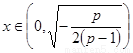 时,
时,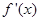 >0;
>0;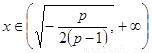 时,
时,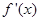 <0.
<0.
故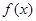 在
在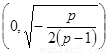 单调递增,在
单调递增,在 单调递减. …………4分
单调递减. …………4分
(2)因为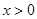 ,所以
,所以
当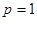 时,
时,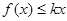 恒成立
恒成立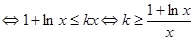
令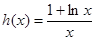 ,则
,则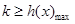 ,
……………6分
,
……………6分
因为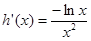 ,由
,由 得
得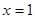 ,
,
且当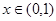 时,
时,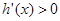 ;当
;当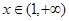 时,
时,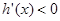 .
.
所以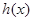 在
在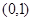 上递增,在
上递增,在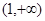 上递减.所以
上递减.所以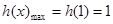 ,
,
故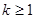 ……………………8分
……………………8分
(3)由(2)知当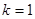 时,有
时,有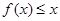 ,当
,当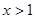 时,
时,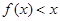 即
即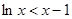 ,
,
令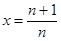 ,则
,则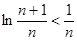 ,即
,即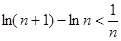 …………10分
…………10分
所以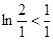 ,
,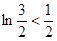 ,…,
,…,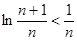 ,
,
相加得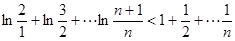
而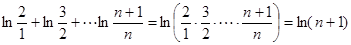
所以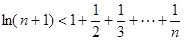 ,
,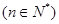 .……………………12分
.……………………12分

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目