题目内容
如图,在三棱锥V-ABC中,已知∠VAB=∠VAC=∠ABC= ,且BC=a,AB=b,AV=c,求:
,且BC=a,AB=b,AV=c,求:

(1)二面角A-VB-C的平面角的度数;
(2)BV与CA夹角的余弦值.
答案:
解析:
提示:
解析:
|
解法1:(1)∵VA⊥AB,VA⊥AC,∴VA⊥平面ABC ∴BC⊥VA,又∵BC⊥AB, ∴平面VBC⊥平面VAB ∴二面角A-VB-C的平面角为 (2)作 ∴BV与CA的夹角为∠ ∵ ∴ 解法2:以B为原点, (1)∵ 又∵BC⊥AB ∴BC⊥平面VAB ∴平面VBC⊥平面VAB ∴二面角A-VB-C的平面角为 (2)cos〈 分析 (1)由BC⊥AB,应用线面垂直、面面垂直的判定定理可证明平面ABC⊥平面VAB. (2)异面直线所成的角需要选择一个点,然后引平行线,做出所成的角. |
提示:
|
本题还可用建立坐标系求解,即以C为原点,CA、CB、 |

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 .
. ,连结
,连结 ,
, ,则
,则 .
. ,设为α.
,设为α. ,
, ,
, =
= =
= ,
, .
. .
. 分别为x轴、y轴、z轴.
分别为x轴、y轴、z轴. 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.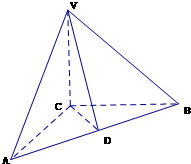 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.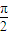 ).
).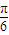 .
.