题目内容
 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.(1)求证:平面VBA⊥平面VBC;
(2)求二面角A-VC-B的平面角的余弦值.
分析:(1)先利用线面垂直的判定,证明BC⊥平面VBA,再利用面面垂直的判定,证明平面VBA⊥平面VBC;
(2)过点B作MB⊥VC于M,过点A作AN⊥VC于N,过点M作MD⊥VC交CA于D,则MD∥NA,∠BMD即为所求,利用余弦定理,即可求得结论.
(2)过点B作MB⊥VC于M,过点A作AN⊥VC于N,过点M作MD⊥VC交CA于D,则MD∥NA,∠BMD即为所求,利用余弦定理,即可求得结论.
解答:(1)证明:∵VA⊥平面ABC,∴VA⊥BC (1分)
∵∠ABC=90°,∴BC⊥AC (2分)
∵VA∩AC=A
∴BC⊥平面VBA (4分)
∵BC?平面VBC
∴平面VBA⊥平面VBC; (5分)
(2)解:过点B作MB⊥VC于M,过点A作AN⊥VC于N,过点M作MD⊥VC交CA于D,则MD∥NA,∠BMD即为所求(7分)
∵∠ABC=90°,且AC=2BC=2VA=4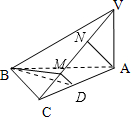
∴VA=VB=2
∴AB=2
(8分)
∵VA⊥平面ABC,∴VA⊥AC,VA⊥AB
∴VC=2
,VB=4 (9分)
∵2
BM=8,2
NA=8,∴BM=AN=
(10分)
∴CM=VN=
=
∴CN=2
-
=
(11分)
∵
=
=
=
∴MD=
,CD=1 (12分)
在△ABC中,∵AC=2BC,∴∠CAB=30°,∴∠ACB=60°
∴BD=
=
(13分)
在△BMD中,cos∠BMD=
=
所以所求二面角的平面角的余弦值是
(14分)
∵∠ABC=90°,∴BC⊥AC (2分)
∵VA∩AC=A
∴BC⊥平面VBA (4分)
∵BC?平面VBC
∴平面VBA⊥平面VBC; (5分)
(2)解:过点B作MB⊥VC于M,过点A作AN⊥VC于N,过点M作MD⊥VC交CA于D,则MD∥NA,∠BMD即为所求(7分)
∵∠ABC=90°,且AC=2BC=2VA=4

∴VA=VB=2
∴AB=2
| 3 |
∵VA⊥平面ABC,∴VA⊥AC,VA⊥AB
∴VC=2
| 5 |
∵2
| 5 |
| 5 |
4
| ||
| 5 |
∴CM=VN=
4-(
|
2
| ||
| 5 |
∴CN=2
| 5 |
2
| ||
| 5 |
8
| ||
| 5 |
∵
| MD |
| NA |
| CM |
| CN |
| CD |
| CA |
| 1 |
| 4 |
∴MD=
| ||
| 5 |
在△ABC中,∵AC=2BC,∴∠CAB=30°,∴∠ACB=60°
∴BD=
| 4+1-2×2×1×cos60° |
| 3 |
在△BMD中,cos∠BMD=
| ||||||||
2×
|
| 1 |
| 4 |
所以所求二面角的平面角的余弦值是
| 1 |
| 4 |
点评:本题考查线面垂直、面面垂直的判定,考查面面角,考查学生分析解决问题的能力,正确作出面面角是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ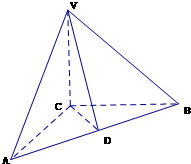 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°. .
.