题目内容
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<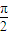 ).
).(Ⅰ)求证:平面VAB⊥平面VCD;
(Ⅱ)当确定角θ的值,使得直线BC与平面VAB所成的角为
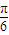 .
.
【答案】分析:法一:(Ⅰ)要证平面VAB⊥平面VCD,只需证明平面VAB内的直线AB,垂直平面VCD内的两条相交直线CD、VC即可;
(Ⅱ)过点C在平面VCD内作CH⊥VD于H,说明∠CBH就是直线BC与平面VAB所成的角.求出 ,使得直线BC与平面VAB所成的角为
,使得直线BC与平面VAB所成的角为 .
.
法二:以CA,CB,CV所在的直线分别为x轴、y轴、z轴,
(Ⅰ) 建立如图所示的空间直角坐标系,证明 ,
, ,推出AB⊥平面VCD,即可证明平面VAB⊥平面VCD.
,推出AB⊥平面VCD,即可证明平面VAB⊥平面VCD.
(Ⅱ)求出平面VAB的一个法向量,利用 ,求出使得直线BC与平面VAB所成的角为
,求出使得直线BC与平面VAB所成的角为 的θ的值.
的θ的值.
解答:解法1:(1)∵AC=BC=a,∴△ABC是等腰三角形,
又D是AB的中点,∴CD⊥AB,
又VC⊥底面ABC,∴VC⊥AB.于是AB⊥平面VCD,
又AB?平面VAB,∴平面VAB⊥平面VCD.
 (2)过点C在平面VCD内作CH⊥VD于H,则由(1)知CH⊥平面VAB.连接BH,
(2)过点C在平面VCD内作CH⊥VD于H,则由(1)知CH⊥平面VAB.连接BH,
于是∠CBH就是直线BC与平面VAB所成的角,依题意 ,所以
,所以
在Rt△CHD中, ;
;
在Rt△BHC中, ,
,
∴ ,
,
∵ ,∴
,∴ ,
,
故当 时,
时,
直线BC与平面VAB所成得角为 .
.
解法2:(1)以CA、CB、CV所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则C(0,0,0),A(a,0,0),B(0,a,0), ,
, ,
,
于是, ,
, ,
, .
.
从而 ,即AB⊥CD.
,即AB⊥CD.
同理 ,
,
即AB⊥VD,又CD∩VD=D,∴AB⊥平面VCD.
又AB?平面VAB,∴平面VAB⊥平面VCD.

(2)设平面VAB的一个法向量为n=(x,y,z)
则由 ,得
,得
可取 ,
,
又 ,
,
于是 =
= ,
,
即 ,
,
∵ ,∴
,∴ ,
,
故当 时,直线BC与平面VAB所成得角为
时,直线BC与平面VAB所成得角为 .
.
解法3:(1)以点D为原点,以DC、DB所在的直线分别为x轴、y轴.
建立如图所示的空间直角坐标系,
则D(0,0,0), ,
, ,
, ,
, ,
,
于是 ,
, ,
, .
.
从而 ,即AB⊥DC,
,即AB⊥DC,
同理 ,即AB⊥DV.
,即AB⊥DV.
又DC∩DV=D,∴AB⊥平面VCD.
又AB?平面VAB,∴平面VAB⊥平面VCD.
(2)设平面VAB的一个法向量为n=(x,y,z),
则由 得
得
取n=(tanθ,0,1),
又 ,于是
,于是 ,
,
即 .
.
又∵ ,∴
,∴ .
.
故当 时,直线BC与平面VAB所成的角为
时,直线BC与平面VAB所成的角为 .
.

点评:本小题主要考查线面关系、直线与平面所成角的有关知识,考查空间想象能力和推理运算能力以及应用向量知识解决数学问题的能力
(Ⅱ)过点C在平面VCD内作CH⊥VD于H,说明∠CBH就是直线BC与平面VAB所成的角.求出
 ,使得直线BC与平面VAB所成的角为
,使得直线BC与平面VAB所成的角为 .
.法二:以CA,CB,CV所在的直线分别为x轴、y轴、z轴,
(Ⅰ) 建立如图所示的空间直角坐标系,证明
 ,
, ,推出AB⊥平面VCD,即可证明平面VAB⊥平面VCD.
,推出AB⊥平面VCD,即可证明平面VAB⊥平面VCD.(Ⅱ)求出平面VAB的一个法向量,利用
 ,求出使得直线BC与平面VAB所成的角为
,求出使得直线BC与平面VAB所成的角为 的θ的值.
的θ的值.解答:解法1:(1)∵AC=BC=a,∴△ABC是等腰三角形,
又D是AB的中点,∴CD⊥AB,
又VC⊥底面ABC,∴VC⊥AB.于是AB⊥平面VCD,
又AB?平面VAB,∴平面VAB⊥平面VCD.
 (2)过点C在平面VCD内作CH⊥VD于H,则由(1)知CH⊥平面VAB.连接BH,
(2)过点C在平面VCD内作CH⊥VD于H,则由(1)知CH⊥平面VAB.连接BH,于是∠CBH就是直线BC与平面VAB所成的角,依题意
 ,所以
,所以在Rt△CHD中,
 ;
;在Rt△BHC中,
 ,
,∴
 ,
,∵
 ,∴
,∴ ,
,故当
 时,
时,直线BC与平面VAB所成得角为
 .
.解法2:(1)以CA、CB、CV所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,
则C(0,0,0),A(a,0,0),B(0,a,0),
 ,
, ,
,于是,
 ,
, ,
, .
.从而
 ,即AB⊥CD.
,即AB⊥CD.同理
 ,
,即AB⊥VD,又CD∩VD=D,∴AB⊥平面VCD.
又AB?平面VAB,∴平面VAB⊥平面VCD.

(2)设平面VAB的一个法向量为n=(x,y,z)
则由
 ,得
,得
可取
 ,
,又
 ,
,于是
 =
= ,
,即
 ,
,∵
 ,∴
,∴ ,
,故当
 时,直线BC与平面VAB所成得角为
时,直线BC与平面VAB所成得角为 .
.解法3:(1)以点D为原点,以DC、DB所在的直线分别为x轴、y轴.
建立如图所示的空间直角坐标系,
则D(0,0,0),
 ,
, ,
, ,
, ,
,于是
 ,
, ,
, .
.从而
 ,即AB⊥DC,
,即AB⊥DC,同理
 ,即AB⊥DV.
,即AB⊥DV.又DC∩DV=D,∴AB⊥平面VCD.
又AB?平面VAB,∴平面VAB⊥平面VCD.
(2)设平面VAB的一个法向量为n=(x,y,z),
则由
 得
得
取n=(tanθ,0,1),
又
 ,于是
,于是 ,
,即
 .
.又∵
 ,∴
,∴ .
.故当
 时,直线BC与平面VAB所成的角为
时,直线BC与平面VAB所成的角为 .
.
点评:本小题主要考查线面关系、直线与平面所成角的有关知识,考查空间想象能力和推理运算能力以及应用向量知识解决数学问题的能力

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.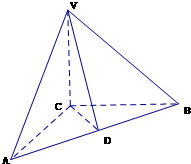 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°. .
.