题目内容
当k∈Z时,在①sin(kπ+A.①和② B.③和④ C.①和④ D.②和③
解析:(1)当k=2n时,sin(kπ+![]() )=sin(2nπ+
)=sin(2nπ+![]() )=sin
)=sin![]() .
.
当k=2n+1时,sin(kπ+![]() )=sin[(2n+1)π+
)=sin[(2n+1)π+![]() ]=sin(2nπ+π+
]=sin(2nπ+π+![]() )=sin(π+
)=sin(π+![]() )=-sin
)=-sin![]() .
.
(2)sin(2kπ±![]() )=sin(±
)=sin(±![]() )=±sin
)=±sin![]() .
.
(3)当k=2n时,sin[kπ+(-1)k·![]() ]=sin[2nπ+(-1)2n·
]=sin[2nπ+(-1)2n·![]() ]=sin
]=sin![]() .
.
当k=2n+1时,sin[kπ+(-1)k·![]() ]=sin[2nπ+π-
]=sin[2nπ+π-![]() ]=sin
]=sin![]() .
.
(4)cos[2kπ+(-1)k·![]() ]=cos[(-1)k·
]=cos[(-1)k·![]() ].
].
当k=2n时,原式=cos![]() =sin
=sin![]() .
.
当k=2n+1时,原式=cos[(-1)2n+1·![]() ]=cos
]=cos![]() =sin
=sin![]() .故选B.
.故选B.
答案:B

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 如图,已知双曲线C1:
如图,已知双曲线C1:
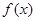 =
= ,给出下列四个命题:
,给出下列四个命题: 为最小正周期的周期函数;
为最小正周期的周期函数;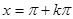 (k∈Z)时,该函数取得最小值-1;
(k∈Z)时,该函数取得最小值-1; (k∈Z)对称;
(k∈Z)对称;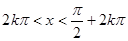 (k∈Z)时,0<
(k∈Z)时,0<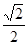 .
.