题目内容
7.已知{an}满足an+1=an+2n,且a1=33,则$\frac{{a}_{n}}{n}$的最小值为$\frac{21}{2}$.分析 利用“累加求和”方法可得an,再利用导数研究函数的单调性即可得出.
解答 解:{an}满足an+1=an+2n,即an+1-an=2n,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=2(n-1)+2(n-2)+…+2×1+33
=2×$\frac{(n-1)n}{2}$+33
=n2-n+33.
则$\frac{{a}_{n}}{n}$=$\frac{{n}^{2}-n+33}{n}$=n+$\frac{33}{n}$-1,
令f(x)=$x+\frac{33}{x}$,(x≥1),则f′(x)=1-$\frac{33}{{x}^{2}}$=$\frac{{x}^{2}-33}{{x}^{2}}$,在x∈$[1,\sqrt{33})$上单调递减;在x∈$(\sqrt{33},+∞)$上单调递增.
f(5)=5+$\frac{33}{5}$=$\frac{58}{5}$,f(6)=6+$\frac{33}{6}$=$\frac{23}{2}$<f(5).
∴n=6时,f(x)取得最小值,因此$\frac{{a}_{n}}{n}$的最小值为$\frac{23}{2}-1$=$\frac{21}{2}$.
故答案为:$\frac{21}{2}$.
点评 本题考查了“累加求和”方法、利用导数研究函数的单调性极值与最值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
17.对某校小学生进行心理障碍测试,得到如下列联表(单位:名)
性别与心理障碍列联表
试说明三种心理障碍分别与性别的关系如何.(我们规定:如果随机变量K2的观测值小于2.076,就认为没有充分的证据显示“两个分类变量有关系”.参考值图表见题3)
性别与心理障碍列联表
| 焦虑 | 说谎 | 懒惰 | 总计 | |
| 女生 | 5 | 10 | 15 | 30 |
| 男生 | 20 | 10 | 50 | 80 |
| 总计 | 25 | 20 | 651 | 110 |
17.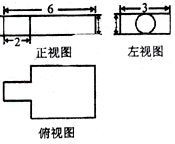 中国古代数学名著《九章算术》中记载了公元前344年 商鞅督造一种标准量器--商鞍铜方升,其三视图如图所示(单位:升),则此量器的体积为(单位:立方升)( )
中国古代数学名著《九章算术》中记载了公元前344年 商鞅督造一种标准量器--商鞍铜方升,其三视图如图所示(单位:升),则此量器的体积为(单位:立方升)( )
 中国古代数学名著《九章算术》中记载了公元前344年 商鞅督造一种标准量器--商鞍铜方升,其三视图如图所示(单位:升),则此量器的体积为(单位:立方升)( )
中国古代数学名著《九章算术》中记载了公元前344年 商鞅督造一种标准量器--商鞍铜方升,其三视图如图所示(单位:升),则此量器的体积为(单位:立方升)( )| A. | 14 | B. | 12+$\frac{π}{2}$ | C. | 12+π | D. | 38+2π |
 观察如图三角形数表,假设第n行第二个数为an(n≥2,n∈N*)
观察如图三角形数表,假设第n行第二个数为an(n≥2,n∈N*)
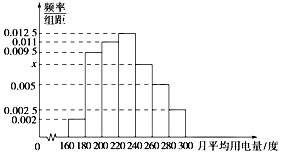 节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
节能减排以来,兰州市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.