题目内容
19．不等式2x2-x-3≥0的解集为{x|x≤-1或x$≥\frac{3}{2}$}．分析 把不等式化为（2x-3）（x+1）≥0，求出不等式对应方程的实数根，写出解集即可．
解答 解：不等式2x2-x-3≥0可化为（2x-3）（x+1）≥0
不等式对应方程的两个实数根分别为$\frac{3}{2}$和-1，
∴不等式的解集为{x|x≤-1或x$≥\frac{3}{2}$}．
故答案为：{x|x≤-1或x$≥\frac{3}{2}$}．
点评 本题考查了一元二次不等式的解法与应用问题，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
9．某班某学习小组共7名同学站在一排照相，要求同学甲和乙必须相邻，同学丙和丁不能相邻，则不同的站法共有（ ）种．
| A． | $A_5^5A_6^2$ | B． | $A_2^2A_4^4A_4^2$ | C． | $A_2^2A_5^5A_6^2$ | D． | $A_2^2A_4^4A_5^2$ |
11．为了普及环保知识，共建美丽宜居城市，某市组织了环保知识竞赛，随机抽取了甲、乙两单位中各5名职工的成绩（单位：分）如下表：
（1）根据表中的数据，分别求出甲、乙两个单位这5名职工成绩的平均数和方差，并判断哪个单位的职工对环保知识掌握得更好；（参考公式：样本数据x1，x2，…，xn的方差：${s^2}=\frac{1}{n}[{（{x_1}-\overline x）^2}+{（{x_2}-\overline x）^2}+…+{（{x_n}-\overline x）^2}]$，其中$\overline x$为样本平均数）
（2）用简单随机抽样法从乙单位5名职工中抽取2名，求抽取的2名职工的成绩差的绝对值至少是4的概率．
| 甲单位 | 87 | 88 | 91 | 91 | 93 |
| 乙单位 | 85 | 89 | 91 | 92 | 93 |
（2）用简单随机抽样法从乙单位5名职工中抽取2名，求抽取的2名职工的成绩差的绝对值至少是4的概率．
8．函数y=ln（3x-x3）的单调递增区间是（ ）
| A． | （0，1） | B． | （-1，1） | C． | $（-\sqrt{3}，-1）$ | D． | $（1，\sqrt{3}）$ |
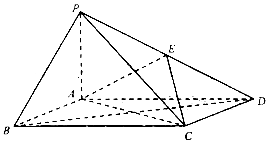如图，在四棱锥P-ABCD中，底面ABCD的平行四边形，∠ADC=60°，$AB=\frac{1}{2}AD$，PA⊥面ABCD，E为PD的中点．