题目内容
直线l经过点P(2,-5),且与点A(3,-2)和B(-1,6)的距离之比为1:2,求直线l的方程.
分析:首先设直线l的方程为y+5=k•(x-2),然后根据点到直线的距离公式得出
=
,求出k的值,即可求出直线方程.
| |k-3| |
| |3k+11| |
| 1 |
| 2 |
解答:解:∵直线l过P(2,-5),
∴可设直线l的方程为y+5=k•(x-2),
即kx-y-2k-5=0.
∴A(3,-2)到直线l的距离为d1=
=
B(-1,6)到直线l的距离为d2=
=
∵d1:d2=1:2
∴
=
∴k2+18k+17=0.
解得k1=-1,k2=-17.
∴所求直线方程为x+y+3=0和17x+y-29=0.
∴可设直线l的方程为y+5=k•(x-2),
即kx-y-2k-5=0.
∴A(3,-2)到直线l的距离为d1=
| |3k+2-2k-5| | ||
|
| |k-3| | ||
|
B(-1,6)到直线l的距离为d2=
| |k•(-1)-6-2k-5| | ||
|
| |3k+11| | ||
|
∵d1:d2=1:2
∴
| |k-3| |
| |3k+11| |
| 1 |
| 2 |
∴k2+18k+17=0.
解得k1=-1,k2=-17.
∴所求直线方程为x+y+3=0和17x+y-29=0.
点评:此题考查了直线的一般方程和点到直线的距离公式,熟练掌握点到直线的距离公式是解题的关键,属于中档题.

练习册系列答案
相关题目
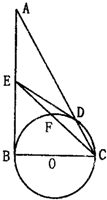 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.