题目内容
16.已知$β∈({\frac{3π}{2},2π})$,满足tan(α+β)-2tanβ=0,则tanα的最小值是$-\frac{{\sqrt{2}}}{4}$.分析 根据题意,利用两角和的正切公式,化为关于tanβ的一元二次方程,利用判别式求出tanα的最小值.
解答 解:∵tan(α+β)-2tanβ=0,
∴tan(α+β)=2tanβ,
∴$\frac{tanα+tanβ}{1-tanαtanβ}$=2tanβ,
∴2tanαtan2β-tanβ+tanα=0,①
∴α,β∈($\frac{3π}{2}$,2π),
∴方程①有两负根,tanα<0,
∴△=1-8tan2α≥0,
∴tan2α≤$\frac{1}{8}$,
∴-$\frac{\sqrt{2}}{4}$≤tanα<0;
即tanα的最小值是-$\frac{\sqrt{2}}{4}$.
故答案为:-$\frac{\sqrt{2}}{4}$.
点评 本题考查两角和与差的正切公式,也考查了一元二次方程与根与系数的应用问题,是综合性题目.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
7.某几何体的三视图如图所示,则这个几何体外接球的表面积为( )
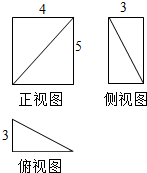

| A. | 20π | B. | 40π | C. | 50π | D. | 60π |
4.若函数$f(x)=\left\{\begin{array}{l}sinx+\frac{3}{2},x≥0\\{x^2}+a,x<0\end{array}\right.$(其中a∈R)的值域为$[\frac{1}{2},+∞)$,则a的取值范围是( )
| A. | $[\frac{3}{2},+∞)$ | B. | $[\frac{1}{2},\frac{3}{2}]$ | C. | $[\frac{1}{2},\frac{5}{2}]$ | D. | $[\frac{1}{2},+∞)$ |
1.“lgx>lgy”是“$\sqrt{x}$>$\sqrt{y}$”的( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要条件 | D. | 既不充分也不必要 |
6.已知$a={(\frac{1}{2})^3},b={3^{\frac{1}{2}}},c={log_{\frac{1}{2}}}3$,则a,b,c之间的大小关系为( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | a>c>b |
 如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.
如图,椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>0,b>0)和圆C2:x2+y2=b2,已知圆C2将椭圆C1的长轴三等分,且圆C2的面积为π,椭圆C1的下顶点为E,过坐标原点O且与坐标轴不重合的任意直线l与圆C2相交于点A、B,直线EA、EB与椭圆C1的另一个交点分别是点P、M.