Question

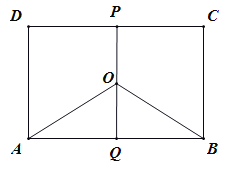
【题目】如图，在四棱锥P－ABCD中，已知底面ABCD是边长为1的正方形，侧面PAD⊥平面ABCD，PA＝PD，PA与平面PBC所成角的正弦值为。

（1）求侧棱PA的长；

（2）设E为AB中点，若PA≥AB，求二面角B－PC－E的余弦值．

Answer 1

【答案】（1）或.（2）

【解析】

（1）取AD中点O．BC中点M，连结OP，OM，证得以O为原点OA，OM，OP为x，y，Z轴建立空间直角坐标系，求得平面PBC的一个法向量，利用向量的夹角公式，即可求解。

（2）由（1）知，得平面PBC的一个法向量为，再求得平面PCE的一个法向量为，利用向量的夹角公式，即可求解二面角的余弦值。

解：（1）取AD中点O．BC中点M，连结OP，OM，

因为PA＝PD，所以

又因为平面PAD⊥平面ABCD，OP平面PAD．平

面平面ABCD＝AD，所以OP⊥平面ABCD

所以

又因为ABCD是正方形，所以,

以O为原点OA，OM，OP为x，y，Z轴建立空间直角

坐标系O－xyz（如图），

则,

设，则,

设平面PBC的一个法向量为,

则有取，则，从而

设PA与平面PBC所成角为，因为

所以

解得或．所以或.

（2）由（1）知，，所以，

由（1）知，平面PBC的一个法向量为，

设平面PCE的一个法向量为,而,

所以取，则，即

设二面角B－PC－E的平面角为，

所以，

根据图形得为锐角，所以二面角B－PC－E的余弦值为