题目内容
如图, 四棱锥P－ABCD的底面ABCD是正方形, PA⊥底面ABCD, E, F分别是AC, PB的中点.
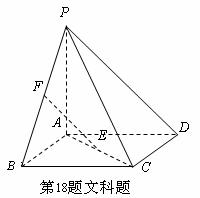(1) 证明: EF∥平面PCD；
(2) 若PA＝AB, 求EF与平面PAC所成角的大小.
(1) 证明: 如图, 连结BD, 则E是BD的中点.
又F是PB的中点,，所以EF∥PD.
因为EF不在平面PCD内,所以EF∥平面PCD.
(2) 连结PE. 因为ABCD是正方形，所以BD⊥AC.
又PA⊥平面ABC，所以PA⊥BD.
因此BD⊥平面PAC.故∠EPD是PD与平面PAC所成的角.
因为EF∥PD,
所以EF与平面PAC所成的角的大小等于∠EPD.
因为PA＝AB＝AD, ∠PAD＝∠BAD＝
,
所以Rt△PAD ≌ Rt△BAD. 因此PD＝BD.
在Rt△PED中,sin∠EPD＝
,得∠EPD=
.
所以EF与平面PAC所成角的大小是.
练习册系列答案
名校课堂系列答案
相关题目
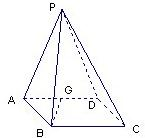如图在四棱锥P-ABCD中，底面ABCD是∠DAB=60°，且边长为a的菱形，侧面PAD为正三角形，其所在平面垂直于底面ABCD．
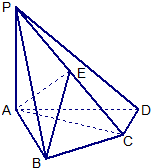如图，四棱锥P-ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．
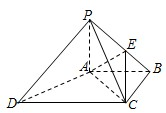如图，四棱锥P-ABCD中，PA⊥底面ABCD，PC⊥AD．底面ABCD为梯形，AB∥DC，AB⊥BC．PA=AB=BC，点E在棱PB上，且PE=2EB．
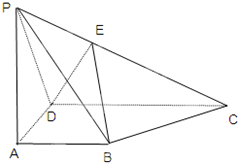如图，四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD为直角梯形，AB∥CD，BA⊥AD，且CD=2AB．
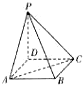如图，四棱锥P-ABCD的底面为正方形，PD⊥底面ABCD，PD=AD=1，设点CG到平面PAB的距离为d1，点B到平面PAC的距离为d2，则有（ ）