Question

一盒中放有大小相同的红色、绿色、黄色三种小球，已知红球个数是绿球个数的两倍，黄球个数是绿球个数的一半．现从该盒中随机取出一个球，若取出红球得1分，取出黄球得0分，取出绿球得－1分，试写出从该盒中取出一球所得分数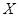的分布列．

 

Answer 1

【答案】

 

	1	0	－1

【解析】

试题分析：欲写出ξ的分布列，要先求出ξ的所有取值，以及ξ取每一值时的概率．

设黄球的个数为，由题意知，绿球个数为，红球个数为，盒中的总数为．

  　∴　，，．

　所以从该盒中随机取出一球所得分数的分布列为

	1	0	－1

考点：本题主要考查离散性随机变量及其分布列。

点评：这是离散性随机变量及其分布列种基本题型，应从分析实际背景出发，运用古典概型计算相应概率，求得分布列。