题目内容
一盒中放有大小相同的红色、绿色、黄色三种小球,已知红球个数是绿球个数的两倍,黄球个数是绿球的一半,现从该盒中随机取出一个球,若取出红球得1分,取出黄球得0分,取出绿球得-1分,试写出从该盒中随机取出一球所得分数ξ的分布列.分析:由题意知,从该盒中随机取出一球,这个球可能是红色或绿色或黄色的,随机取出一球所得分数ξ的可能取值是-1,0,1,根据等可能事件的概率得到分布.
解答:解:设黄球的个数为n,依题意知道绿球个数为2n,
红球个数为4n,盒中球的总数为7n.
由题意知,从该盒中随机取出一球,这个球可能是红色或绿色或黄色的,
∴随机取出一球所得分数ξ的可能取值是-1,0,1,
根据等可能事件的概率得到,
∴P(ξ=1)=
=
,P(ξ=-1)=
=
,P(ξ=0)=
=
∴从该盒中随机取出一球所得分数ξ的分布列为:

红球个数为4n,盒中球的总数为7n.
由题意知,从该盒中随机取出一球,这个球可能是红色或绿色或黄色的,
∴随机取出一球所得分数ξ的可能取值是-1,0,1,
根据等可能事件的概率得到,
∴P(ξ=1)=
| 4n |
| 7n |
| 4 |
| 7 |
| 2n |
| 7n |
| 2 |
| 7 |
| n |
| 7n |
| 1 |
| 7 |
∴从该盒中随机取出一球所得分数ξ的分布列为:

点评:本题考查等可能事件的概率和离散型随机变量的分布列,求离散型随机变量的分布列和期望是近年来理科高考必出的一个问题,题目做起来不难,运算量也不大,是一道必得分的题目.

练习册系列答案
相关题目
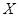 的分布列.
的分布列.