题目内容
已知函数![]() 和
和![]() 的图像关于原点对称,且
的图像关于原点对称,且![]() ;
;
(1)、求函数![]() 的解析式;
的解析式;
(2)、解不等式![]() >
>![]() ;
;
(3)、若![]() 在[-1,1]上是增函数,求实数
在[-1,1]上是增函数,求实数![]() 的取值范围。
的取值范围。
解析: (1)设函数y=f(x)的图像上任一点Q(x0 , y0),关于原点的对称点是P(x , y)
则  即
即 
∵点Q(x0 , y0)在y=f(x)的图像上,
∴![]()
![]() , 即
, 即 ![]() ∴
∴![]() ;
;
(2)由![]()
![]() 可得
可得 ![]() ;
;
当![]() 时,有
时,有 ![]() 此时不等式无解
此时不等式无解
当![]() 1时,有
1时,有 ![]() ,∴
,∴ ![]() ;
;
因此,原不等式的解集是[![]() ,
,![]() ];
];
(3)由题设知:![]() ,
,
若![]() 时,
时,![]() ,在[
,在[![]() ,1]上是增函数,∴
,1]上是增函数,∴ ![]() ;
;
若![]() 时,对称轴的方程为
时,对称轴的方程为 ![]() ,
,
当![]()
![]() 时,则
时,则 ![]()
![]()
![]() ,解得:
,解得:![]()
![]() ,
,
当![]()
![]() 时,则
时,则 ![]()
![]()
![]() ,解得:
,解得: ![]()
![]()
![]() ,
,
综上所述,实数![]() 的取值范围是(
的取值范围是(![]() ,0] 。
,0] 。

练习册系列答案
相关题目
 :“函数
:“函数 和
和 的图像关于
的图像关于 轴对称”,则
轴对称”,则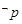 是 命题;(填“真”或“假” )
是 命题;(填“真”或“假” )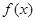 和
和 的图像关于原点对称,且
的图像关于原点对称,且 .
. ;
; 在区间
在区间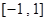 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围. :“函数
:“函数 和
和 的图像关于
的图像关于 轴对称”,则
轴对称”,则 是 命题;(填“真”或“假” )
是 命题;(填“真”或“假” )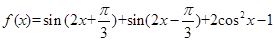 ,
, .
. 求函数
求函数 的最小正周期;
的最小正周期; 若函数
若函数 的图像和
的图像和 的图像关于直线
的图像关于直线 对称,求
对称,求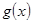 在
在 上的最大值和最小值.
上的最大值和最小值.