题目内容
已知f(x)=4+ax-1的图象恒过定点P,则点P的坐标是
- A.(1,5)
- B.(1,4)
- C.(0,4)
- D.(4,0)
A
解析:
分析:由x-1=0得x=1,代入解析式求出对应的函数值,就是此点的坐标.
解答:令x-1=0,解得x=1,代入f(x)=4+ax-1得,f(1)=5,则函数f(x)过定点(1,5).故选A.
点评:本题考查了指数函数过定点(0,1),即令指数为零求出对应的x和y的值,即所求的定点坐标.
解析:
分析:由x-1=0得x=1,代入解析式求出对应的函数值,就是此点的坐标.
解答:令x-1=0,解得x=1,代入f(x)=4+ax-1得,f(1)=5,则函数f(x)过定点(1,5).故选A.
点评:本题考查了指数函数过定点(0,1),即令指数为零求出对应的x和y的值,即所求的定点坐标.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
已知f(x)=
是R上的增函数,则a的范围是( )
|
| A、(0,6) |
| B、[0,6) |
| C、[1,6) |
| D、(1,6] |
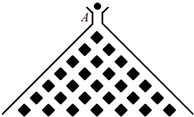 (2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是
(2011•丹东模拟)如图,在竖直平面内有一个“游戏滑道”,空白部分表示光滑滑道,黑色正方形表示障碍物,自上而下第一行有1个障碍物,第二行有2个障碍物,…,依此类推.一个半径适当的光滑均匀小球从入口A投入滑道,小球将自由下落,已知小球每次遇到正方形障碍物上顶点时,向左、右两边下落的概率都是