题目内容
12．
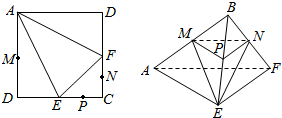如图，在边长为2的正方形ABCD中，E，F分别为CD，BC的中点，M，N，P分别为AD，CF，CE的中点，现沿AE，AF，EF折叠，使B，C，D三点重合，构成一个三棱锥B-AEF．（1）求证：平面MNP∥平面AEF；
（2）求三棱锥P-MNE的体积．
分析 （1）根据中位线定理得MP∥AE，PN∥EF，故平面MNP∥平面AEF；
（2）把△PNE看做棱锥的底面，则棱锥的高为MB，代入体积公式计算．
解答 证明：（1）∵M，P，分别是AB，BE的中点，∴MP∥AE，
∵AE?平面AEF，MP?平面AEF，
∴MP∥平面AEF，
同理可得：NP∥平面AEF，又∵MP?平面MNP，NP?平面MNP，MP∩NP=P，
∴平面MNP∥平面AEF．
（2）∵P，N是BE，BF的中点，∴S△PNE=$\frac{1}{4}$S△BEF=$\frac{1}{4}×\frac{1}{2}×1×1$=$\frac{1}{8}$．
∵AB⊥BE，AB⊥BF，BE∩BF=B，BE?平面BEF，BF?平面BEF，∴AB⊥平面BEF，
∴三棱锥P-MNE的体积V=$\frac{1}{3}$S△PNE•MB=$\frac{1}{3}×\frac{1}{8}×1$=$\frac{1}{24}$．
点评 本题考查了面面平行的判定，棱锥的体积计算，属于中档题．
练习册系列答案
相关题目
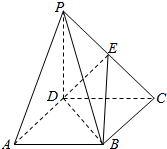如图，已知四棱锥P-ABCD的底面是矩形，PD⊥平面ABCD，PD=CD，点E是PC的中点，连接DE、BD、BE．
分别是
内角
的对边，
．
，求
；
，且
，求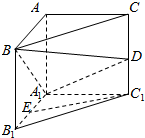
在直三棱柱ABC-A1B1C1中，∠BAC=90°，D，E分别为CC1和A1B1的中点，且A1A=AC=2AB=2．
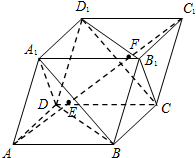如图，已知平行六面体ABCD-A1B1C1D1中，AC1与平面A1BD、CB1D1交于点E、F两点．设K为△B1CD1的外心，则VK-BED：${V_{{A_1}-BFD}}$=$\frac{1}{3}$．
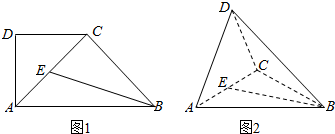如图1，在直角梯形ABCD中，∠ADC=90°，CD∥AB，AD=CD=$\frac{1}{2}$AB=2，点E为AC中点．将△ADC沿AC折起，使平面ADC⊥平面ABC，得到几何体D-ABC，如图2所示．
如图所示，四边形MNPQ为圆内接四边形，对角线MP与NQ相交于点S，R为MN与QP延长线的交点，且MN=NP，∠MPQ=60°，△MPR为等腰三角形．