题目内容
3．已知函数f（x）=$\frac{6cos（π+x）+5si{n}^{2}（π-x）-4}{cos（2π-x）}$，且f（m）=2，试求f（-m）的值．分析 根据函数的奇偶性求解即可．
解答 解：因为f（x）=$\frac{6cosx+5si{n}^{2}x-4}{cosx}$=f（-x），
所以f（x）是偶函数，
又f（m）=2，
故f（-m）=2
点评 本题主要考查的奇偶性，属于基础题．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
15．定义行列式运算：$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3．若将函数f（x）=$|\begin{array}{l}{sinx}&{cosx}\\{\sqrt{3}}&{1}\end{array}|$的图象向左平移m（m＞0）个单位后，所得图象对应的函数为奇函数，则m的最小值是（ ）
| A． | $\frac{2π}{3}$ | B． | $\frac{π}{6}$ | C． | $\frac{5}{6}$π | D． | $\frac{π}{3}$ |
12．
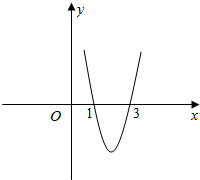已知奇函数f（x）在（0，+∞）上的图象如图所示，则不等式$\frac{f（x）}{x-1}＜0$的解集为（ ）
已知奇函数f（x）在（0，+∞）上的图象如图所示，则不等式$\frac{f（x）}{x-1}＜0$的解集为（ ）| A． | （-3，-1）∪（0，1）∪（1，3） | B． | （-3，-1）∪（0，1）∪（3，+∞） | C． | （-∞，-3）∪（-1，0）∪（3，+∞） | D． | （-∞，-3）∪（-1，0）∪（0，1） |