题目内容
9.设$n=\int_0^{\frac{π}{2}}{4sinxdx}$,则二项式${({x-\frac{2}{x}})^n}$的展开式的常数项是24.分析 先利用定积分求出n=4,在二项式展开式的通项公式中,令x的幂指数等于0,求得r的值,即可求得展开式中的常数项的值.
解答 解:∵$n=\int_0^{\frac{π}{2}}{4sinxdx}$=-4cosx${|}_{0}^{\frac{π}{2}}$=0+4=4,则二项式${({x-\frac{2}{x}})^n}$=${(x-\frac{2}{x})}^{4}$ 的展开式的通项公式为Tr+1=${C}_{4}^{r}$•x4-r•${(-\frac{2}{x})}^{r}$=${C}_{4}^{r}$•(-2)r•x4-2r,
令4-2r=0,求得r=2,可得常数项为 ${C}_{4}^{2}$•4=24,
故答案为:24.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
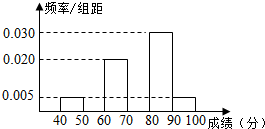 某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),已知成绩在[50,60 )的学生有9人,
某学校团委组织了“文明出行,爱我中华”的知识竞赛,从参加考试的学生中抽出60名学生,将其成绩(单位:分)整理后,得到如下频率分布直方图(其中分组区间为[40,50),[50,60),…,[90,100]),已知成绩在[50,60 )的学生有9人,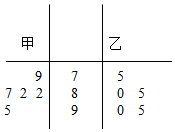 甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:
甲、乙两位学生参加某项竞赛培训,在培训期间,他们参加的5项预赛成绩的茎叶图记录如下:



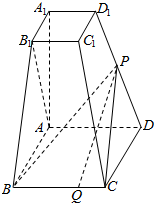 已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点,Q为BC边上的一点.
已知四棱台ABCD-A1B1C1D1的上下底面分别是边长为2和4的正方形,AA1=4且AA1⊥底面ABCD,点P为DD1的中点,Q为BC边上的一点.