题目内容
如果曲线y=x2+x-3的某一条切线与直线y=3x+4平行,求切点坐标与切线方程.
答案:
解析:
解析:
|
解:设切点P(x0,y0), 则 = = = = =1+2x0. ∵所求切线与直线y=3x+4平行, ∴1+2x0=3. ∴x0=1. ∴y0=-1. ∴切点坐标为(1,-1),切线方程为y+1=3(x-1),即3x-y-4=0. 解析:设切点P(x0,y0),根据导数的几何性质求出P点坐标,再由点斜式得方程. |

练习册系列答案
相关题目
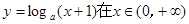 内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围
内单调递减,q:曲线y=x2+(2a-3)x+1与x轴交于不同的两点.如果p与q有且只有一个正确,求a的取值范围