Question

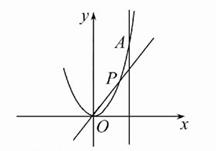
设点P在曲线y＝x²上，从原点向A(2,4)移动，如果直线OP，曲线y＝x²及直线x＝2所围成的封闭图形的面积分别记为S₁，S₂.

(1)当S₁＝S₂时，求点P的坐标；

(2)当S₁＋S₂有最小值时，求点P的坐标和最小值.,

Answer 1

【解析】(1)设点P的横坐标为t(0<t<2)，则P点的坐标为(t，t²)，直线OP的方程为y＝tx，

S₁＝

S₂＝

因为S₁＝S₂，所以t＝，点P的坐标为

(2)S＝S₁＋S₂＝

S′＝t²－2，令S′＝0得t²－2＝0，t＝，

因为0<t<时，S′<0；<t<2时，S′>0，

所以，当t＝时，S_min＝，点P的坐标为(,2).

【变式备选】求由抛物线y²＝8x(y>0)与直线x＋y－6＝0及y＝0所围成的图形的面积.

【解析】由题意，作出图形(如图所示)，

解方程组

所以y²＝8x(y>0)与直线x＋y－6＝0的交点为(2,4)，

所以所求面积为S=